1. দৃঢ় বস্তুর ঘূর্ণন-সঠিক উত্তরটি বেছে নাও।
1. “m” গ্রাম ভরের তিনটি “a” cm বাহু বিশিষ্ট একটি সমবাহু ত্রিভুজ ∆ABC – এর তিনটি শীর্ষ আছে। ABC তলে AB এর লম্ব দিকে AX এর সাপেক্ষে তন্ত্রটির জড়তা ভ্রামক কত (gcm2 এককে) হবে- (A) 2 ma^2 ~ ~(B) \frac{3}{2} ma^2 ~ ~(C) \frac{3}{4} ma^2 ~~(D) \frac{5}{4} ma^2 [WBJEE,22]
AX থেকে A বিন্দুর দূরত্ব=0
AX থেকে B বিন্দুর দূরত্ব= a
AX\থেকে A বিন্দুর দূরত্ব= \frac{a}{2}
নির্ণেয় জড়তা ভ্রামক= m0^2+ma^2+m{(\frac{a}{2})}^2=ma^2+m{(\frac{a}{4})}^2=\frac{5ma^2}{4}
3.দৃঢ় বস্তুর ঘূর্ণন- সংক্ষিপ্ত প্রশ্নোত্তর
3.1 একটি l দৈর্ঘ্যের দন্ড খাড়া দাঁড় করানো আছে। দন্ডটি ছেড়ে দিলে সেটি মাটিতে পড়ল। দন্ডটির উপরের প্রান্ত মাটিতে কত বেগে আঘাত করবে?
=> উল্লম্ব অবস্থায় দন্ডের ভর কেন্দ্রের সাপেক্ষে স্থিতিশক্তি mg(\frac{l}{2})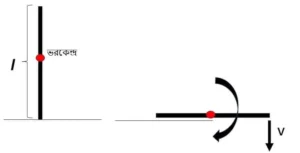
প্রান্তবিন্দুর সাপেক্ষে ঘূর্ণায়মান দন্ডের জড়তা ভ্রামক I=\frac{1}{12}ml^2+m(\frac{l}{2})^2=\frac{1}{3}ml^2। মাটিতে আঘাত করার সময় দন্ডের ঘূর্ণনের জন্য গতিশক্তি=\frac{1}{2}I\omega^2
শক্তির সংরক্ষণ নীতি অনুযায়ী,
\frac{1}{2}I\omega^2=\frac{l}{2}mg
or, \frac{mr^2}{3}\omega^2=mgl
or, \omega r=\sqrt{3gl}
or, v=\sqrt{3gl}\;[\because v=\omega r]
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠