2.1 এই মহাবিশ্বে কি পরম স্থির বস্তু আছে?
=> না। মহাবিশ্বে পরম স্থির বস্তু বলে কিছু নেই।

2.2 পৃথিবীর সাপেক্ষে হিমালয় পর্বত স্থির না গতিশীল?
=> স্থির

2.3 ঘড়ির কাঁটার গতি কী প্রকৃতির?
=> ঘূর্ণন গতি।

2.4 সূর্যের চারপাশে পৃথিবীর ঘূর্ণন কী প্রকৃতির গতি?
=> বৃত্তীয় গতি।

2.5 মিশ্র গতির উদাহরণ দাও।
=> গাড়ির চাকা।

2.6 ঘূর্ণায়মান লাট্টুর গতি কীরূপ?
=>ঘূর্ণন গতি।

2.7 সরলদোল গতির উদাহরণ দাও।
=> পেন্ডুলাম। 

2.8 অতিক্রান্ত দূরত্ব স্কেলার  না ভেক্টর রাশি?
=> স্কেলার রাশি।

2.9 অতিক্রান্ত দূরত্বের SI ও CGS একক কী?
=> SI একক- m ও CGS একক- cm।

2.10 সরণ স্কেলার  না ভেক্টর রাশি?
=> ভেক্টর রাশি।

2.11 সরণের SI ও CGS একক কী?
=>SI একক- m ও CGS একক- cm।

2.12 দ্রুতি স্কেলার  না ভেক্টর রাশি?
=> স্কেলার রাশি

2.13 দ্রুতির SI ও CGS একক কী?
=> SI একক- m/s ও CGS একক- cm/s।

2.14 বেগ স্কেলার  না ভেক্টর রাশি?
=> ভেক্টর রাশি।

2.15 বেগের SI ও CGS একক কী?
=. SI একক- m/s ও CGS একক- cm/s।

2.16 কোন্ ক্ষেত্রে গতিশীল বস্তুর দ্রুতি ও বেগ একই হয় ?
=> বস্তুটি যদি সরলরেখা বরাবর গতিশীল হয় তবে দ্রুতি ও বেগ একই হবে।

2.17 ত্বরণ স্কেলার  না ভেক্টর রাশি?
=> ভেক্টর রাশি।

2.18 ত্বরণের SI ও CGS একক কী?
=> SI একক- m/s^2 ও CGS একক- cm/s^2।

2.19 বেগ ও সময়ের লেখচিত্র কী প্রকাশ করে?
=> সরণকে নির্দেশ করে।

2.20 ত্বরণ ও সময়ের লেখচিত্র কী প্রকাশ করে?
=> বেগের পরিবর্তনকে নির্দেশ করে।

2.21 শূন্যস্থান পূরণ করো: মন্দনকে ___ ত্বরণ বলা হয়।
=> ঋণাত্মক।

2.22 নিউটনের প্রথম গতিসূত্র থেকে কী কী জানা যায়?
=> জাড্য ধর্ম ও বলের সংজ্ঞা।

2.23 নিউটনের কোন্ সূত্র থেকে বলের সংজ্ঞা পাওয়া যায়?
=> নিউটনের প্রথম গতিসূত্র থেকে বল সম্পর্কে ধারনা পাওয়া যায়। সেই ধারণা থেকেই বলের সংজ্ঞা দেওয়া যায়।

2.24 শূন্যস্থান পূরণ করো : বস্তুর______জাড্যের পরিমাপ।
=> ভর

2.25 একটি গাড়ি হঠাৎ চলতে শুরু করলে যাত্রীদের মাথা পেছনের দিকে সরে যায়। এটি কোন জাড্যের পরিবর্তন নির্দেশ করে?
=> স্থিতিজাড্য থেকে গতিজাড্যে পরিণত হয়।

2.26 নিউটনের দ্বিতীয় গতিসূত্র থেকে কী জানা যায়?
=> বলের পরিমাপ জানা যায়।

2.27 বল স্কেলার  না ভেক্টর রাশি?
=> ভেক্টর রাশি।

2.28 বলের SI ও CGS একক কী?
=> SI একক- N ও CGS একক- dyne।

2.29 ভরবেগ স্কেলার  না ভেক্টর রাশি?
=> ভেক্টর রাশি।

2.30 ভরবেগের SI ও CGS একক কী?
=> SI একক- kg.m/s ও CGS একক- g.cm/s।

2.31 নিউটনের কোন্ গতিসূত্র থেকে রৈখিক ভরবেগ সংরক্ষণ সূত্রটি প্রতিষ্ঠিত হয়?
=> দ্বিতীয় গতিসূত্র থেকে।

2.32 নিউটনের কোন গতি সূত্র থেকে ভরবেগের পরিমাপ করা যায়?
=> দ্বিতীয় গতিসূত্র থেকে। 

2.33 শূন্যস্থান পূরণ কর। 1N= __ dyne।
=> 10^5

2.34 ভরবেগের মাত্রা লেখো।
=> [MLT^{-1}]

2.35 বলের মাত্রা লেখো।
=> [MLT^{-2}]

2.36 শূন্যস্থান পূরণ করো- সামান্তরিকের সূত্রের সাহায্যে দুটি বলের ____ নির্ণয় করা যায়।
=> লব্ধি।

2.37 সুতোর সাহায্যে 100 গ্রাম ভরের একটি বস্তু ঝুলছে। সুতোর টান কত?
=> 100g.wt = 100✕980 dyne =98000 dyne।

2.38 রোলার টানা সহজ না খেলা সহজ?
=> টানা সহজ।

2.39 দুটি বিকর্ষণধর্মী বলের উদাহরণ দাও।
= কুলম্বীয় তড়িৎ বল ও কুলম্বীয় চৌম্বক বল। 

2.40 ঘর্ষণ বল কোন দিকে ক্রিয়া করে?
=> গতির বিপরীত দিকে ক্রিয়া করে।

2.41 বন্দুক থেকে গুলি ছুঁড়লে বন্দুকটি পিছনে সরে যায়। এই ঘটনাটি কীসের দ্বারা ব্যাখ্যা করা যায়?
=> নিউটনের তৃতীয় গতিসূত্র বা  রৈখিক ভরবেগের সংরক্ষণ সূত্র দ্বারা ব্যাখ্যা করা যায়।

3.1 নির্দেশতন্ত্র কাকে বলে?
=>  বস্তু স্থির বা গতিশীল অবস্থার নির্ধারণের জন্য একটি স্থির বস্তুর প্রয়োজন। যার সাপেক্ষে অন্যান্য বস্তুর স্থিরতা বা গতিশীলতা নির্ধারণ করা হয়।  এই স্থির বস্তুকে বলা হয় নির্দেশ বস্তু।  নির্দেশ বস্তুর সঙ্গে সংযুক্ত স্থানাঙ্ক ব্যবস্থাকে নির্দেশ তন্ত্র বলা হয়।

3.2 চলন গতি কাকে বলে? উদাহরণ দাও।
=> দুটি বস্তুকণার গতি যদি পরস্পরের সমান্তরাল থাকে তাহলে একে চলন গতি বলে।
যেমন- একটি বইকে সোজা পথে নিয়ে গেলে বইয়ের প্রতিটি কণা পরস্পরের সমান্তরালে থাকে। এক্ষেত্রে বইয়ের গতিকে চলন গতি বলা যায়।

3.3 ঘূর্ণন গতি কাকে বলে? উদাহরণ দাও।
=> বস্তুকণাসমষ্টি একটি নির্দিষ্ট বিন্দু বা অক্ষের চারপাশে ঘুরতে থাকলে একে ঘূর্ণন গতি বলে।
যেমন-  নিজের অক্ষের চারপাশে পৃথিবীর ঘূর্ণন।

3.4 বৃত্তীয় গতি কাকে বলে?  উদাহরণ দাও।
=>  কোনো বস্তু একটি নির্দিষ্ট বিন্দু বা অক্ষের চারপাশে বৃত্তাকার পথে ঘুরতে থাকলে তাকে বৃত্তীয় গতি বলে।
যেমন- সূর্যের চারপাশে পৃথিবীর গতি।

 3.5 বৃত্তীয় গতি ও ঘূর্ণন গতির মধ্যে পার্থক্য লেখো।
=> 

ঘূর্ণন গতি	বৃত্তীয় গতি
i) বস্তুকণাসমষ্টি একটি নির্দিষ্ট বিন্দু বা অক্ষের চারপাশে ঘুরতে থাকলে একে ঘূর্ণন গতি বলে।	i) কোনো বস্তু একটি নির্দিষ্ট বিন্দু বা অক্ষের চারপাশে বৃত্তাকার পথে ঘটতে থাকলে তাকে বৃত্তীয় গতি বলে।
ii) এই গতির ক্ষেত্রে বস্তুকে বিন্দু হিসেবে ধরা হয় না।	ii) এক্ষেত্রে বস্তুকে বিন্দু হিসেবে ধরা হয়।
iii) এক্ষেত্রে বস্তু সমষ্টির সমগ্র ভর ঘূর্ণন অক্ষের কোনো বিন্দুতে বা কেন্দ্রে অবস্থান করে।	iii) কেন্দ্রবিন্দুতে সমগ্র ভর থাকে না।

3.6 অতিক্রান্ত দূরত্ব কাকে বলে? এর SI ও CGS একক লেখ।  এটি স্কেলার না ভেক্টর রাশি?
=> কোনো বস্তুকণা নির্দিষ্ট সময়ে যে পথ অতিক্রম করে তাকে অতিক্রান্ত দূরত্ব বলে।
SI একক m ও CGS একক cm।
অতিক্রান্ত দূরত্ব স্কেলার রাশি।

3.7 সরণ কাকে বলে? এর SI ও CGS একক লেখ।  এটি স্কেলার না ভেক্টর রাশি?
=> কোনো বস্তুকণা নির্দিষ্ট দিকে যে দূরত্ব যায় তাকে সরণ বলে।
SI একক m ও CGS একক cm।
সরণ ভেক্টর রাশি।

3.8 দ্রুতি (speed) কাকে বলে? এর SI ও CGS একক লেখ।  এটি স্কেলার না ভেক্টর রাশি?
=> কোনো বস্তুকণা একক সময়ে যে দূরত্ব অতিক্রম করে তাকে দ্রুতি বলে।
SI একক m/s ও CGS একক cm/s।
দ্রুতি স্কেলার রাশি।

3.9 বেগ (velocity) কাকে বলে? এর SI ও CGS একক লেখ।  এটি স্কেলার না ভেক্টর রাশি?
=> একক সময়ে বস্তুর যে সরণ ঘটে থাকে বেগ বলে।
SI একক m/s ও CGS একক cm/s।
বেগ ভেক্টর রাশি।

3.10 গড়বেগ বলতে কী বোঝায়?
=>  যাত্রা পথের মোট সরণকে মোট সময় দিয়ে ভাগ করলে যে রাশি পাওয়া যায় তাকে গড়বেগ বলে।

3.11 দ্রুতি ও বেগের মধ্যে পার্থক্য লেখো।
=> 

দ্রুতি	বেগ
i) কোনো বস্তুকণা একক সময়ে যে দূরত্ব অতিক্রম করে তাকে দ্রুতি বলে।	i) একক সময়ে বস্তুর যে সরণ ঘটে থাকে বেগ বলে।
ii) দ্রুতি স্কেলার রাশি।	ii) বেগ ভেক্টর রাশি।
iii) গতিশীল বস্তুর দ্রুতি শূন্য হয় না।	iii) গতিশীল বস্তুর বেগ শূন্য হতে পারে।

3.12 ত্বরণ (acceleration) কাকে বলে? এর SI ও CGS একক লেখ।  এটি স্কেলার না ভেক্টর রাশি?
=> বেগ বৃদ্ধির হারকে ত্বরণ বলে।
SI একক m/s^2 ও CGS একক cm/s^2।
ত্বরণ ভেক্টর রাশি।

3.13 ত্বরণের এককে দুটি সেকেন্ড থাকে কেন?
=> একটি সেকেন্ড বেগকে প্রকাশ করে এবং অপর সেকেন্ডটি বেগের পরিবর্তনকে প্রকাশ করে।

3.14 মন্দন কাকে বলে? এর SI ও CGS একক লেখো।
=> বেগ হ্রাসের হারকে মন্দন বলে।
SI একক m/s^2 ও CGS একক cm/s^2।

3.15 মন্দনকে ঋণাত্মক ত্বরণ বলা হয় কেন?
=>  ত্বরণ যেমন বৃদ্ধির হার তেমনই মন্দন হল বেগ হ্রাসের হার।  অর্থাৎ ত্বরণ ও মন্দন একই ব্যাপার শুধু এদের দিক বিপরীত। তাই মন্দনকে ঋণাত্মক ত্বরণ বলা হয়।

3.16 প্রমাণ কর: v=u+at; চিহ্নগুলি প্রচলিত অর্থ বহন করে।
=> u=প্রাথমিক বেগ, v= অন্তিম বেগ হলে
বেগের পরিবর্তন = v-u। এর জন্য t সময় লাগলে
ত্বরণ, a=\frac{v-u}{t}
or, v-u=at
or, v=u+at
3.17 সুষম ত্বরণে গতিশীল কণার v-t লেখচিত্র অঙ্কণ কর।
=>

 

3.18 প্রমাণ কর: s=ut+\frac{1}{2}at^2; চিহ্নগুলি প্রচলিত অর্থ বহন করে।
=> ধরি, v= অন্তিম বেগ। কণাটি সুষম ত্বরণে থাকায়  সমগ্র যাত্রাপথে এর গড়বেগ হবে-v_a=\frac{v+u}{2}
কণার মোট সরণ=গড়বেগ✕সময়
or, s=v_a \times t
or, \;\;\;=\frac{v+u}{2}t
or, \;\;\;=\frac{u+at+u}{2}t  [∵v=u+at]
or, \;\;\;=\frac{2u+at}{2}t
or, \;\;\;=ut+\frac{1}{2}at^2

3.19 প্রমাণ কর: v^2=u^2+2as; চিহ্নগুলি প্রচলিত অর্থ বহন করে।
=> আমরা জানি,  v=u+at; যেখানে t= সময়
v^2=(u+at)^2   [উভয়পাশে বর্গ করে পাই]
or, \;\;\;=u^2+2uat+a^2t^2
or, \;\;\;=u^2+2a(ut+\frac{1}{2}at^2)
or, v^2=u^2+2as     [∵s=ut+\frac{1}{2}at^2]

3.20 লেখচিত্রের সাহায্যে প্রমাণ কর-s=ut+\frac{1}{2}at^2; চিহ্নগুলি প্রচলিত অর্থ বহন করে।
=>
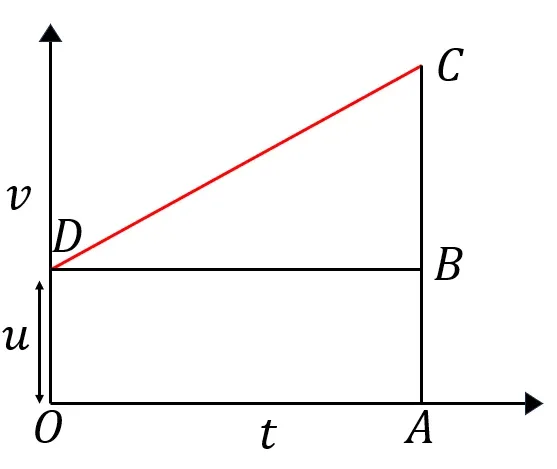
লেখচিত্র অনুযায়ী- OD=BA=u, OA=DB=t, CA=v
তাহলে, BC=CA-BA=v-u
আমরা জানি, বেগ ও সময়ের লেখচিত্র সরণকে নির্দেশ করে।
∴ s= OACD চতুর্ভুজের ক্ষেত্রফল
      =OABD চতুর্ভুজের ক্ষেত্রফল+△BDC-এর ক্ষেত্রফল
    = OD.OA+\frac{1}{2}BD.CB
    =ut+\frac{1}{2}.t.(v-u)
    =ut+\frac{1}{2}.\frac{(v-u)}{t}.t^2
  ∴s =ut+\frac{1}{2}.a.t^2    [∵v=u+at    or, a=\frac{v-u}{t}]

3.21 লেখচিত্রের সাহায্যে প্রমাণ কর-v^2=u^2+2as; চিহ্নগুলি প্রচলিত অর্থ বহন করে।
=>
চিত্র অনুযায়ী- CO=u, AB=v, OC=t
আমরা জানি, বেগ ও সময়ের লেখচিত্র সরণকে নির্দেশ করে।
s= OABC ট্রাপিজিয়ামের ক্ষেত্রফল
আবার, কোনো ট্রাপিজিয়ামের ক্ষেত্রফল= \frac{1}{2}✕সমান্তরাল বাহুদ্বয়ের যোগফল ✕ সমান্তরাল বাহুদ্বয়ের দূরত্ব
∴ s=\frac{1}{2}\times(OC+AB)\times OA
or,  s=\frac{1}{2}\times(u+v)\times t
or,  2s=(v+u)\times (v-u)    [∵v=u+at    or, t=\frac{v-u}{a}]
or,  2s=(v+u).\frac{(v-u)}{t}
or,  2as=v^2-u^2
∴ v^2=u^2+2as

3.22 ভরবেগ কাকে বলে? ভরবেগ স্কেলার না ভেক্টর রাশি? – ব্যাখ্যা দাও।
=> ভর ও বেগের সমন্বয়ে বস্তুতে যে ধর্মের সৃষ্টি হয় তাকে ভরবেগ বলে।
ভরবেগ= ভর×বেগ। ভর স্কেলার রাশি হলেও বেগ ভেক্টর রাশি। তাই এদের গুণফল ভেক্টর রাশিই হবে। বেগের অভিমুখ ও ভরবেগের অভিমুখ একই দিকে হয়।

3.23 নিউটনের প্রথম গতিসূত্রটি লেখো।
=> বাইরে থেকে বল প্রয়োগ না করলে স্থির বস্তু চিরকাল স্থির থাকবে এবং গতিশীল বস্তু একই বেগে সরলরেখায় চলতে থাকবে।

3.24 নিউটনের প্রথম গতিসূত্র থেকে কীসের কীসের ধারণা পাওয়া যায়?
=> বলের সংজ্ঞা ও জাড্য ধর্মের ধারণা পাওয়া যায়। 

3.25 নিউটনের প্রথম গতিসূত্র থেকে বলের সংজ্ঞা দাও। 
=> যে কারণের জন্য স্থির বস্তু গতিশীল হয় অথবা গতিশীল বস্তু স্থির হয় কিংবা বেগের পরিবর্তন হয় তাকে বল বলে। 

3.26 জাড্য ধর্ম কী? জাড্য কয় প্রকার ও কী কী?
=> স্থির বস্তু স্থির থাকার কিংবা গতিশীল বস্তুর গতীয় অবস্থায় থাকার যে ধর্ম একেই জাড্য বলে।
জাড্য দুই প্রকার। স্থিতিজাড্য ও গতিজাড্য।

3.27 স্থিতিজাড্য কাকে বলে? উদাহরণ দাও।
=> স্থির বস্তুর স্থির থাকার ধর্মকে স্থিতিজাড্য বলে।
স্থির বাস হঠাৎ চলতে শুরু করলে যাত্রীদের মাথা পেছনের দিকে হেলে যায়।  বাস হঠাৎ চলতে শুরু করলে যাত্রীদের পা গতিশীল অবস্থাতে থাকলেও মাথা স্থির অবস্থাতেই থাকতে চায়। সেই জন্য মাথা পিছনের দিকে হেলে যায়।

3.28 গতিজাড্য কাকে বলে? উদাহরণ দাও।
=> গতিশীল বস্তুর গতি ও অবস্থায় থাকার প্রবণতাকে গতিজাড্য বলে।
গতিশীল বাস হঠাৎ থেমে গেলে যাত্রীদের মাথা সামনের দিকে হেলে যায়। বাস থেমে গেলে যাত্রীদের পা বাসের সাথে যুক্ত থাকায় পায়ের অংশ থেমে যায়। কিন্তু তখনও যাত্রীদের মাথা গতিশীল থাকায় এই মাথা সামনের দিকে ঝুকে যায়।

3.29 কার্যকর বল কাকে বলে?
=> বাইরের থেকে বল প্রয়োগ করলে যদি বস্তু সরলরেখা বরাবর চলতে শুরু করে তাহলে একে কার্যকর বল বলে। 

3.30 প্রতিমিত বল কাকে বলে? 
=> যে বলের প্রভাবে বস্তুর আকার বা আকৃতি বা উভয়েরই পরিবর্তন ঘটে তাকে প্রতিমিত বল বলে। 

3.31 বল সংযোজন এর সামান্তরিক সূত্রটি লেখো। চিত্রসহ ব্যাখ্যা কর।
=> একটি বিন্দু থেকে নির্গত দুটি বল যদি সামান্তরিকের দুটি সন্নিহিত বাহু দ্বারা নির্দেশিত হয় তবে ওই বিন্দু থেকে নির্গত সামান্তরিকের কর্ণটি উক্ত বলদ্বয়ের লব্ধিকে প্রকাশ করবে।

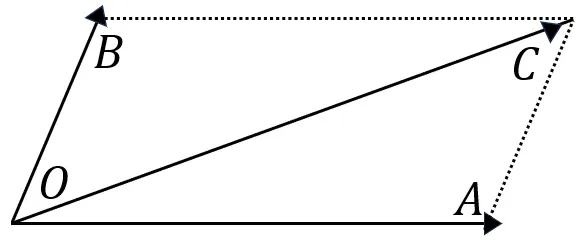
চিত্রে \overrightarrow{OA} ও \overrightarrow{OB} দুটি বল O বিন্দু থেকে নির্গত হচ্ছে। OA ও OB হল সামান্তরিকে দুই সন্নিহিত বাহু। তাহলে OC কর্ণটি এই দুই বলের লব্ধিকে প্রকাশ করবে। অর্থাৎ, \overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}

3.32 রোলারকে ঠেলা অপেক্ষা টানা সহজ কেন?
=>
F= রোলার প্রযুক্ত বল, W= রোলারের ওজন, H= প্রযুক্ত বলের অনুভূমিক উপাংশ, V= প্রযুক্ত বলের উল্লম্ব উপাংশ।
চিত্র অনুযায়ী দেখা যাচ্ছে রোলার ঠেললে ওজনের সঙ্গে প্রযুক্ত বলের উল্লম্ব উপাংশ যোগ হয়। তাই রোলার আপাত ওজন বৃদ্ধি পায় ও ঠেলতে অসুবিধা হয়। অন্যদিকে, রোলার টানলে ওজনের সঙ্গে প্রযুক্ত বলের উল্লম্ব উপাংশ বিয়োগ হয়। তাই রোলার আপাত ওজন হ্রাস পায় ও রোলারকে এগিয়ে নিয়ে যেতে সুবিধা হয়।

3.33 ভরবেগ কাকে বলে? এর SI ও CGS একক লেখক? এর মাত্রা নির্ণয় করো। এটি স্কেলার না ভেক্টর রাশি?
=> ভর ও বেগের সমন্বয়ে বস্তুর যে ধর্ম তৈরি হয় তাকে ভরবেগ বলে। ভরবেগ= ভর×বেগ=m×v
SI একক kg.m/s। CGS একক g.cm/s
মাত্রা [MLT^{-1}]
ভরবেগ ভেক্টর রাশি।

3.34 নিউটনের দ্বিতীয় গতি সূত্রটি লেখো।
=> কোনো বস্তুর ওপর প্রযুক্ত বল বস্তুটিরর ভরবেগের পরিবর্তনের হারের সঙ্গে সমানুপাতি এবং বল যেদিকে ক্রিয়া করে বস্তুর ভরবেগের পরিবর্তনও সে দিকে ঘটে।

3.35 নিউটনের দ্বিতীয় গতিসূত্র থেকে বলের রাশিমালা নির্ণয় কর।
=> ধরি, একটি বস্তুকণার ভর m। এরমধ্যে F বল প্রয়োগ করলে বস্তুটির বেগ u থেকে v হয় এবং এর জন্য প্রয়োজনীয় সময় লাগে t। বস্তুটির ত্বরণ হবে a=\frac{v-u}{t}
এখন, বস্তুটির প্রাথমিক ভরবে mu এবং অন্তিম ভরবেগ mv। ভরবেগের পরিবর্তন mv-mu= m(v-u)।
ভরবেগের পরিবর্তনের হার= \frac{m(v-u)}{t}
নিউটনের দ্বিতীয় গতিসূত্র অনুযায়ী, F\propto \frac{m(v-u)}{t}
or, F=km \frac{(v-u)}{t}    [k=সমানুপাতী ধ্রুবক]
or, F=kma      (1)
বলের সংজ্ঞা এমন ভাবে নেওয়া হয় যে m=1 ও a=1 হলে F=1 হয়।
(1) নং সমীকরণে মানগুলি বসিয়ে দিয়ে পাওয়া যায় k=1।
 সুতরাং, F=ma

3.36 বল স্কেলার না ভেক্টর রাশি? বলের SI ও CGS একক গুলি কী কী? বলের মাত্রা লেখো। 
=> বল হলো ভেক্টর রাশি।
বলের  SI একক kg.m/s^2 বা নিউটন (N)  ও CGS একক g.cm/s^2 বা ডাইন‌(dyne)।
বলের মাত্রা [MLT^{-2}]

3.37 1 নিউটন কাকে বলে?
=>1 kg ভরের বস্তুর ওপর যে বল প্রয়োগ করলে এর মধ্যে 1 m/s² ত্বরণ সৃষ্টি হয় তাহলে তাকে 1 নিউটন বলে।

3.38 1 ডাইন কাকে বলে?
=> 1 g ভরের বস্তুর ওপর যে বল প্রয়োগ করলে এর মধ্যে 1 cm/s² ত্বরণ সৃষ্টি হয় তাহলে তাকে 1 ডাইন বলে।

3.39 নিউটন ও ডাইনের মধ্যে সম্পর্ক টি দেখাও।
=>1N =1kg.m/s² =1kg.1m/s² = 1000g×100cm/s² =100000 g.cm/s² =10⁵ dyne

3.40 নিউটনের দ্বিতীয় গতিসূত্র থেকে প্রথম গতিসূত্র প্রতিষ্ঠা করো।
=> ধরি, m ভরের একটি বস্তুর উপর F বল প্রয়োগ করায় সেটির বেগ t সময়ে u থেকে v হয়। কণাটির সুষম ত্বরণ a।
নিউটনের দ্বিতীয় গতিসূত্র অনুযায়ী বল F=ma
F=0 হলে,  ma=0
or, a=0  [∵m≠0]
or, \frac{v-u}{t}=0
or, v-u=0
∴ v=u
অর্থাৎ বলের অনুপস্থিতিতে বস্তুর বেগ অপরিবর্তিত থাকে।

3.41 ভরকে জাড্যের পরিমাপ বলা হয় কেন?
=> নিউটনের দ্বিতীয় গতিসূত্র অনুযায়ী জানা যায় যে, নির্দিষ্ট পরিমাণ বল প্রয়োগের ক্ষেত্রে ভর যত বাড়বে ত্বরণ ততই কমে। অর্থাৎ বস্তুর ভর যত বেশি হবে তার বেগের পরিবর্তন করার জন্য তত বেশি বল প্রয়োগ করা দরকার। বেগ পরিবর্তন মানে জাড্যের পরিবর্তন। তাই ভরকে জাড্যের পরিমাপ বলা হয়।

3.42 জড়ত্বীয় ভর কাকে বলে?
=> কোনো বস্তুর ওপর বল প্রয়োগ করে তার জাড্য ধর্মের পরিবর্তন করার সময় যে বাঁধা পাওয়া যায় তা যে রাশির মাধ্যমে প্রকাশ করা হয় তাকে জড়ত্বীয় ভর বলে।

3.43 নিউটনের তৃতীয় গতিসূত্রটি লেখো।
=> প্রত্যেক ক্রিয়ারই সমান ও বিপরীত প্রতিক্রিয়া আছে। 

3.44 রকেটের কার্যনীতি ব্যাখ্যা করো।
=> রকেট বা জেট বিমানে জ্বালানি দহনের ফলে উচ্চ গতিতে নির্গত হয়। এটি হলো ক্রিয়া। এর ফলে রকেটের উপর একটি প্রতিক্রিয়া সৃষ্টি হয় যা রকেটকে সামনের দিকে এগিয়ে নিয়ে যায়। দাহ্য জ্বালানি যত দ্রুত বের হবে রকেট ততই দ্রুত গতিতে সামনের দিকে এগোতে থাকবে। 

3.45 কয়েকটি স্পর্শজনিত বল এবং অস্পর্শ জনিত বলের উদাহরণ দাও।
=> স্পর্শজনিত বল- টান, ধাক্কা, ঘর্ষণ, ঘাত ইত্যাদি।
অস্পর্শজনিত বল- কুলম্বীয় তড়িৎ বল, কুলম্বীয় চুম্বক বল, মহাকর্ষ বল ইত্যাদি। 

3.46 রৈখিক ভরবেগের সংরক্ষণ সূত্রটি বিবৃতি কর।
=> বাইরে থেকে বল প্রয়োগ না করলে কোনো বস্তু সংস্থার মোট রৈখিক ভরবেগ সর্বদা অপরিবর্তিত থাকে অর্থাৎ সংঘর্ষের আগে ও সংঘর্ষের পরে  মোট রৈখিক ভরবেগ একই থাকে।

3.47 রৈখিক ভরবেগের সংরক্ষণ সূত্রের গাণিতিক রূপটি লেখ।
=> ধরি, A ও B বস্তুর ভর যথাক্রমে m_1 ও m_2। এদের প্রাথমিক বেগ যথাক্রমে u_1 ও u_2।  t সময় পরে বস্তু দুটি সংঘর্ষ ঘটায় এবং বেগ লাভ করে যথাক্রমে v_1 ও v_2। সংঘর্ষের আগে মোট ভরবেগ m_1u_1+m_2u_2। সংঘর্ষের পরে মোট ভরবেগ m_1v_1+m_2v_2। রৈখিক ভরবেগের সংরক্ষণ সূত্র অনুযায়ী-
m_1u_1+m_2u_2=m_1v_1+m_2v_2

3.48 নিউটনের তৃতীয় গতিসূত্র থেকে রৈখিক ভরবেগের সংরক্ষণ সূত্রটি প্রতিষ্ঠা কর।
=>
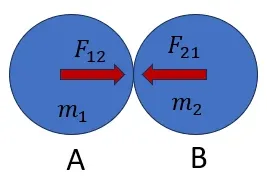
ধরি, A বস্তুর ভর m_1। যা u_1 বেগে ধাবিত হয়ে t সময় পরে m_2 ভরের B বস্তুর সংঘর্ষ ঘটায় এবং v_1 বেগ লাভ করে। A বস্তুর ত্বরণ a_1=\frac{v_1-u_1}{t}। তাহলে, B বস্তু দ্বারা A বস্তুর ওপর প্রযুক্ত বল F_{21}=m_1a_1 = m_1(\frac{v_1-u_1}{t})।
একইভাবে, B  বস্তুর ভর m_2। যা u_2 বেগে ধাবিত হয়ে t সময় পরে A বস্তুর সংঘর্ষ ঘটায় এবং v_2 বেগ লাভ করে। তাহলে A বস্তু দ্বারা B বস্তুর ওপর প্রযুক্ত বল F_{12}=m_2a_2 = m_2(\frac{v_2-u_2}{t})।
নিউটনের দ্বিতীয় গতিসূত্র অনুযায়ী-
F_{21}={-F}_{12}
or, m_1(\frac{v_1-u_1}{t})=-\ m_2(\frac{v_2-u_2}{t})
or, m_1 (v_1-u_1)=-m_2 (v_2-u_2)
or, m_1v_1-m_1u_1=-m_2v_2+m_2u_2
or, m_1v_1+m_2v_2=m_2u_2+m_1u_1  (প্রমাণিত)

3.49 রৈখিক ভরবেগের সংরক্ষণ সূত্র থেকে নিউটনের তৃতীয় গতি সূত্রটি প্রতিষ্ঠা কর। 

=>

ধরি, A বস্তুর ভর m_1। যা u_1 বেগে ধাবিত হয়ে t সময় পরে m_2 ভরের B বস্তুর সংঘর্ষ ঘটায় এবং v_1 বেগ লাভ করে। A বস্তুর ত্বরণ a_1=\frac{v_1-u_1}{t}। তাহলে, B বস্তু দ্বারা A বস্তুর ওপর প্রযুক্ত বল F_{21}=m_1a_1 = m_1(\frac{v_1-u_1}{t})।
একইভাবে, B  বস্তুর ভর m_2। যা u_2 বেগে ধাবিত হয়ে t সময় পরে A বস্তুর সংঘর্ষ ঘটায় এবং v_2 বেগ লাভ করে। তাহলে A বস্তু দ্বারা B বস্তুর ওপর প্রযুক্ত বল F_{12}=m_2a_2 = m_2(\frac{v_2-u_2}{t})।
নিউটনের দ্বিতীয় গতিসূত্র অনুযায়ী-
or, m_1v_1+m_2v_2=m_2u_2+m_1u_1
or, m_1v_1-m_1u_1=-m_2v_2+m_2u_2
or, m_1 (v_1-u_1)=-m_2 (v_2-u_2)
or, m_1(\frac{v_1-u_1}{t})=-\ m_2(\frac{v_2-u_2}{t})
F_{21}={-F}_{12} (প্রমাণিত)

3.50 বন্দুক থেকে গুলি ছুড়লে বন্দুক পিছনের দিকে সরে যায় কেন?
=> গুলিসহ বন্দুক প্রথম অবস্থায় স্থির থাকে।  বন্দুক থেকে যখন গুলি নির্গত হয় তখন গুলির ভর অল্প হলেও বেগ খুব বেশি হয়। তাই গুলির ভরবেগ অনেকটাই হয়।  রৈখিক ভরবেগের সংরক্ষণ সূত্র অনুযায়ী, সংঘর্ষের আগে ও সংঘর্ষের পরে মোট ভরবেগ একই থাকে। সেজন্য গুলি নির্গত হওয়ার সাথে সাথে বিপরীত দিকে বন্দুক সরে আসে। বন্দুকের ভর গুলির তুলনায় বেশি হওয়ায় এর বেগ গুলির তুলনায় অনেকটাই কম হয়। তবে বন্দুক এবং ছুটন্ত গুলির মোট ভরবেগের সমান এবং বিপরীতমুখী হবে।

3.51 বেগ শূন্য অথচ ত্বরণ বর্তমান – এমন একটি ঘটনার উদাহরণ দাও ।
=> একটি বস্তুকে উপরে নিক্ষেপ করলে সর্বোচ্চ বিন্দুতে বেগ শূন্য হয়ে যায়। কিন্তু অভিকর্ষজ ত্বরণ নীচের দিকে ক্রিয়াশীল থাকে।