2. Current Electricity (প্রবাহী তড়িৎ)-যথাযথ উত্তর দাও।
প্রবাহী তড়িৎ
2.1 2Ω রোধের মধ্য দিয়ে তড়িৎপ্রবাহ পাঠানোর জন্য 1.5V তড়িৎচালক বল, 0.5Ω অভ্যন্তরীণ রোধবিশিষ্ট 36 টি সদৃশ কোশে দেওয়া আছে। সর্বোচ্চ তড়িৎপ্রবাহ পাওয়ার জন্য সব থেকে ভালোভাবে কীভাবে কোশগুলিকে যুক্ত করা যাবে? বহিবর্তনীতে প্রবাহমাত্রার মান কত ?
=>
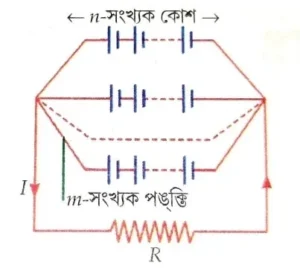মিশ্র সমবায়ের প্রবাহমাত্রা I = \frac{mnE}{mR + nr} = \frac{mnE}{(\sqrt{mR} - \sqrt{nr})^2 + 2\sqrt{mnRr}}
I সর্বোচ্চ হওয়ার শর্ত হল (\sqrt{mR} - \sqrt{nr})^2=0 or, mR=nr or, R = \frac{nr}{m}
এখন, R= 2Ω, r= 0.5Ω,
তাহলে, 2 = \frac{n\times0.5}{m} or, 4m=n
আবার, mn=36 টি কোশ।
তাহলে, m×4m=36 or, m2 = 9 or, m=3
এবং, n= 4×3=12
∴ সর্বোচ্চ তড়িৎপ্রবাহের জন্য 12 টি কোশ শ্রেণি সমবায়ে ও এরকম 3 টি পঙ্ক্তি সমান্তরাল সমবায়ে যুক্ত অরতে হবে।
সর্বোচ্চ প্রবাহমাত্রা, I= \frac{3\times12\times1.5}{3\times2 + 12\times0.5}A = 4.5A
2.2 কোনো তড়িৎবর্তনীতে e তড়িৎচালক বল বিশিষ্ট দুটি তড়িৎকোশকে শ্রেণি সমবায়ে বহিস্থ R রোধের সঙ্গে যুক্ত করা হল। কোশদ্বয়ের অভ্যন্তরীণ রোধ যথাক্রমে r1 ও r2 । প্রবাহ চলাকালীন যদি প্রথম কোশের প্রান্তীয় বিভবপার্থক্য শূন্য হয় তবে R এবং r1 ও r2 –এর মধ্যে সম্পর্ক কী হবে?
=> বর্তনী দিয়ে তড়িৎ প্রবাহ \frac{e+e}{R+r_1+r_2}=\frac{2e}{R+r_1+r_2}
প্রথম কোশে বিভব,
V=e-Ir_1=e-\frac{2er_1}{R+r_1+r_2}=e\frac{R+r_1+r_2-2r_1}{R+r_1+r_2}=e\frac{R+r_2-r_1}{R+r_1+r_2}
কিন্তু, V=0
or, e\frac{R+r_2-r_1}{R+r_1+r_2}=0
or, R+r_2-r_1=0
or, R=r_1-r_2
2.3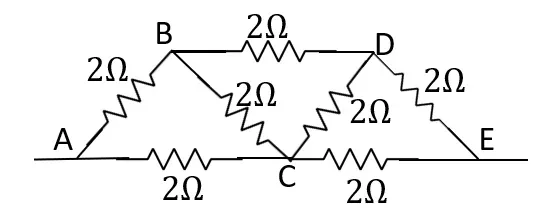 
প্রদত্ত বর্তনির তুল্য রোধ নির্ণয় কর।
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠