Table of Contents
Toggle1. গোলীয় তলে আলোর প্রতিফলন-অতি সংক্ষিপ্ত প্রশ্নোত্তর ( Marks-1)
গোলীয় তলে আলোর প্রতিফলন
1.1 কোন ধরনের গোলীয় দর্পণে দৃশ্যমান ক্ষেত্র সর্বোচ্চ হয়?
=> উত্তল দর্পণ।
1.2 কোন শর্তে একটি অবতল দর্পণ অসদ্বিম্ব গঠন করতে পারে?
=> বস্তু যখন মেরু ও ফোকাসের মাঝামাঝি অবস্থান করে।
1.3 বস্তুর সমান আকারের প্রতিবিম্ব পেতে হলে একটি বস্তুকে গোলীয় দর্পণের কোথায় রাখতে হবে?
=> দর্পণটি হতে হবে অবতল প্রকৃতির। বস্তুকে বক্রতা কেন্দ্রে রাখতে হবে।
1.4 একটি অবতল দর্পণের ক্ষেত্রে একটি সদ্ বস্তু ও তার সদ্ প্রতিবিম্ব দূরত্ব যথাক্রমে u ও v হলে \frac{1}{v}\sim \frac{1}{u} এর লেখচিত্র কিরূপ হবে?
=>  ব্যাখ্যা জানতে এখানে ক্লিক করুন
ব্যাখ্যা জানতে এখানে ক্লিক করুন
1.5 কোনো বস্তুকে অবতল দর্পণের ফোকাস ও মেরুর ঠিক মাঝখানে রাখলে প্রতিবিম্বের বিবর্ধন কত হবে?
=> দ্বিগুণ হবে।
ব্যাখ্যা জানতে এখানে ক্লিক করুন।
1.6 যদি এক জোড়া যুগ্ম বিন্দু কোনো দর্পণের একই দিকে থাকে তাহলে দর্পণটি কী প্রকৃতির?
=> অবতল।
1.7 আলোর তরঙ্গ দৈর্ঘ্য বাড়লে একটি গোলীয় দর্পণের ফোকাস দৈর্ঘের কী পরিবর্তন হয়?
=> অপরিবর্তিত থাকে।
1.8 গোলীয় দর্পণ কর্তৃক গঠিত প্রতিবিম্বের কোন ত্রুটি থাকে না?
=> বর্ণাপেরণ
1.9 f ফোকাস দৈর্ঘ্যের কোনো অবতল দর্পণ থেকে কত দূরত্বে একটি বস্তু রাখলে n বিবর্ধন যুক্ত সদ বিম্ব গঠিত হবে?
=> u=\frac{(n+1)f}{n}
ব্যাখ্যা জানতে এখানে ক্লিক করুন।
1.10 গোলীয় দর্পণের অনুবন্ধী ফোকাস যুগল কী?
=> এটি দর্পণের এমন দুটি বিন্দু যেখানে বস্তু রাখলে অপর স্থানে প্রতিবিম্ব সৃষ্টি হবে।
2. গোলীয় তলে আলোর প্রতিফলন-সংক্ষিপ্ত প্রশ্নোত্তর (Marks-2)
গোলীয় তলে আলোর প্রতিফলন
2.1 সমতল দর্পণে কি সদবিম্ব তৈরি হতে পারে? চিত্র সহযোগী যুক্তি দাও।
=> 
সমতল দর্পণে সদ্ বস্তুর সর্বদা অসদ্ প্রতিবিম্বই তৈরি হবে। তবে বস্তুটি অসদ্ হয় তাহলে সদ্ প্রতিবিম্ব তৈরি হবে। অসদ্ বলতে বোঝানো হচ্ছে রশ্মিগুলি যদি অভিসারী হয়। এর কারণ হল সমতল দর্পণে কোনো রশ্মিকে ফোকাস করা যায় না।
2.2 একটি সমতল দর্পণ থেকে প্রতিফলনের পরে আলোকরশ্মির চ্যুতি কী পরিমাণ হবে?
=> 
চিত্র অনুযায়ী AB রশ্মি MN দর্পণে প্রতিফলিত হয়ে BC পথে যায়। আপতন কোণ i হলে ∠ABC= 2i। ∴ রশ্মির মোট চ্যুতি 180°-2i
2.3 একটি রশ্মিকে স্থির রেখে একটি দর্পণকে যদি θ কোণে ঘোরানো হয় তাহলে প্রতিফলিত রশ্মি 2θ কোণে ঘুরে যায়, প্রমাণ কর।
=>  MN সমতল দর্পণে AB রশ্মির আপতন কোণ ∠ABP = প্রতিফলন কোণ ∠PCB = i
MN সমতল দর্পণে AB রশ্মির আপতন কোণ ∠ABP = প্রতিফলন কোণ ∠PCB = i
দর্পণটি θ কোণে ঘুরে গেলে নতুন অবস্থান হয় M’N’। ∠MBM’=θ। তাহলে PB অভিলম্বটিও ঘুরে যাবে θ কোণে। ∴ ∠PBP’=θ।
এর জন্য প্রতিফলিত রশ্মিটি BC’ পথে গেলে বিচ্যুতি কোণ= ∠CBC’ = ∠PBC-∠PBC’
এখন নতুন আপতন কোণ ∠ABP’=∠ABP-∠P’BP=i-θ।
সুতরাং, নতুন প্রতিফলন কোণ= ∠P’BC’=i-θ
তাহলে ∠PBC’= ∠P’BC’-∠P’BP= (i-θ)-θ=i-2θ
প্রতিফলিত রশ্মির বিচ্যুতি = ∠CBC’ = ∠PBC-∠PBC’=i-( i-2θ)= 2θ (প্রমাণিত)
2.4 অবতল দর্পণের সমীকরণ থেকে নিউটনের সমীকরণ ব্যাখ্যা কর।
=> 
নিউটনের সমীকরণ অনুযায়ী xy=f2। (চিহ্নগুলি প্রচলিত অর্থ বহন করে)
এর অর্থ হল f এর মান ধনাত্মক বা ঋণাত্মক যাই হোক না কেন f2 সর্বদা ধনাত্মক হবে। অর্থাৎ x ধনাত্মক হলে y-ও ধনাত্মক হবে কিংবা x ঋণাত্মক হলে y ও ঋণাত্মক হবে। এর অর্থ হল, ফোকাসের একই পাশ বস্তু ও প্রতিবিম্ব অবস্থান করে।
আবার বস্তু যদি ফোকাস ও মেরুর মাঝে থাকতে তাহলে উৎপন্ন প্রতিবিম্ব অসদ্ হবে মানে দর্পণের অভ্যন্তরে হত। অর্থাৎ ফোকাসের একই পাশে বস্তু ও প্রতিবিম্ব থাকছে।
2.5 দেখাও যে গোলীয় দর্পণের ক্ষেত্রে অনুদৈর্ঘ্য বিবর্ধন সংখ্যা গত ভাবে রৈখিক বিবর্ধনের বর্গের সমান।
=> গোলীয় দর্পণে বস্তু দূরত্ব, প্রতিবিম্ব দূরত্ব ও ফোকাস দূরত্বের মধ্যে সম্পর্ক হল- \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
অক্ষ বরাবর বস্তুকে কিছুটা সরালে প্রতিবিম্বেরও কিছুটা সরণ ঘটবে। যদি du পরিমাণ বস্তুর সরণের জন্য dv পরিমাণ প্রতিবিবিম্বের সরণ হয় তাহলে; অনুদৈর্ঘ্য বা অক্ষীয় বিবর্ধন হল m^\prime=\frac{dv}{du}
এখন, \frac{d}{du}(\frac{1}{v}+\frac{1}{u})=\frac{d}{du}(\frac{1}{f})=0
or, -\frac{1}{v^2}\frac{dv}{du}-\frac{1}{u^2}=0
or, \frac{dv}{du}=-(\frac{v}{u})^2
or, m^\prime=-m^2
যেখানে m^\prime=\frac{dv}{du}= বস্তুর অনুদৈর্ঘ্য বিবর্ধন এবং m=\frac{v}{u}= রৈখিক বিবর্ধন।
2.6 কোনো গোলীয় উত্তল দর্পণের সামনে u দূরত্বে l দৈর্ঘ্যের কোনো বস্তুকে প্রধান অক্ষের উপর লম্বভাবে রাখলে দেখাও যে, প্রতিবিম্বের দৈর্ঘ্য =\frac{fl}{u+f} যেখানে f হল গোলীয় দর্পণের ফোকাস দৈর্ঘ্য।
=>
 উত্তল দর্পণের সমীকরণ- \frac{1}{v}-\frac{1}{u}=\frac{1}{f}
উত্তল দর্পণের সমীকরণ- \frac{1}{v}-\frac{1}{u}=\frac{1}{f}
or, \frac{u}{v}-1=\frac{u}{f}
or, \frac{1}{m}-1=\frac{u}{f} [m=\frac{v}{u}]
or, \frac{1}{m}=\frac{u}{f}+1
or, \frac{1}{m}=\frac{u+f}{f}
or, m=\frac{f}{f+u}
আবার, m =\frac{প্রতিবিম্বের\; দৈর্ঘ্য}{বস্তুর\; দৈর্ঘ্য}=\frac{f}{f+u}
∴ \frac{প্রতিবিম্বের\; দৈর্ঘ্য}{l}=\frac{f}{f+u}
or, প্রতিবিম্বের\; দৈর্ঘ্য=\frac{fl}{f+u} (প্রমাণিত)
2.7 একটি দর্পণ সমতল, উত্তল, নাকি অবতল কীভাবে চিনবে?
=> একটি বস্তুকে দূর থেকে কাছে নিয়ে যেতে হবে। যদি প্রতিবিম্ব সদ্ ও আকারে বস্তুর দৈর্ঘ্যের সমান হয় তাহলে দর্পণটি সমতল। যদি সর্বদা প্রতিবিম্বটি আকারে ছোটোই থাকে তাহলে সেটি উত্তল। আর যদি প্রতিবিম্ব প্রথমে অবশীর্ষ ও পরে সমশীর্ষ হয় তাহলে দর্পণটি অবতল প্রকৃতির হবে।
2.8 উত্তল দর্পণ কখন সদবিম্ব গঠন করে?
=> 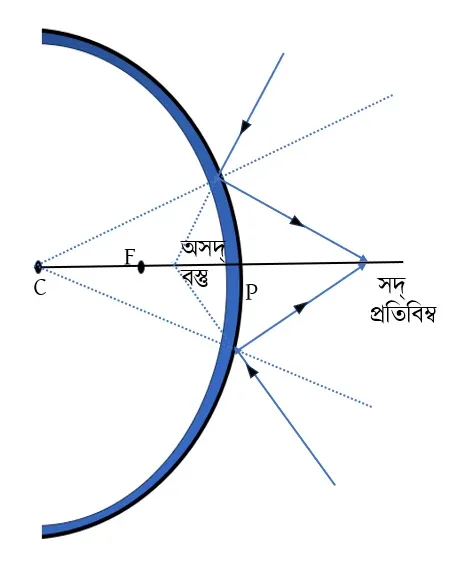
যখন বস্তু অসদ্ অর্থাৎ অভিসারী রশ্মি আপতিত হয় তাহলে সদবিম্ব তৈরি হবে।
2.9 দেখাও যে, অবতল দর্পণের কেন্দ্রে কোনো বস্তু রাখলে তার প্রতিবিম্বের দৈর্ঘ্য একই হবে।
=>
এক্ষেত্রে বস্তু দূরত্ব u=-2f, ফোকাস দূরত্ব= -f
গোলীয় দর্পণের সমীকরণ- \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{v}+\frac{1}{-2f}=\frac{1}{-f}
or, \frac{1}{v}=\frac{1}{-2f}
or, v=-2f
বিবর্ধন m=\frac{v}{u}=-\frac{2f}{2f}=-1 অর্থাৎ, বস্তু ও প্রতিবিম্বের দৈর্ঘ্য একই হবে।
2.10 একটি অবতল দর্পণে গঠিত বস্তুর সদ্ প্রতিবিম্ব এবং ওই বস্তুর মধ্যবর্তী সর্বনিম্ন দূরত্ব কত হতে পারে এবং এটি কখন সম্ভব?
=> সদ্ প্রতিবিম্ব এবং বস্তুর মধ্যবর্তী সর্বনিম্ন দূরত্ব হবে শূন্য। ∴ v-u=0 or, v=u
দর্পণের সমীকরণ, \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{u}+\frac{1}{u}=-\frac{1}{f} [যেহেতু, অবতল দর্পণের ফোকাস দৈর্ঘ্য -ve ও প্রশ্নানুযায়ী v=u]
or, u=-2f=-r
∴ অবতল দর্পণে যদি বস্তু বক্রতাকেন্দ্রে অবস্থান করে তাহলে বস্তু ও প্রতিবিম্বের আকার সমান হবে।
3. গোলীয় তলে আলোর প্রতিফলন-সংক্ষিপ্ত প্রশ্নোত্তর (Marks-3)
গোলীয় তলে আলোর প্রতিফলন
3.1 সমতল দর্পণে একটি আলোক বিন্দুর প্রতিবিম্বের গঠন চিত্র রশ্মি সহযোগে দেখাও।
=> 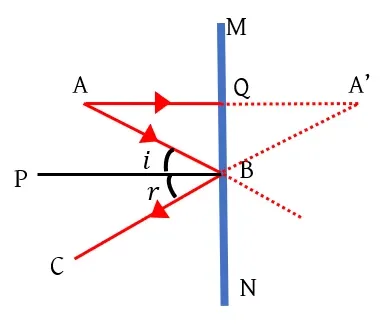
MN সমতল দর্পণে A বিন্দু থেকে একটি রশ্মি দর্পণের Q বিন্দুতে লম্বভাবে পরে। A বিন্দু থেকে নির্গত অপর একটি রশ্মি দর্পণের B বিন্দুতে i কোণে আপতিত হলে BC পথে প্রতিফলিত হয়। প্রতিফলন কোণ r। প্রতিফলনের সূত্র অনুযায়ী i=r।
AQ ও CB কে বর্ধিত করলে A' বিন্দুতে মিলিত হয়। এটিই হল A বিন্দুর প্রতিবিম্ব।
3.2 দিক চিহ্ন সংক্রান্ত নিয়ম এবং আরোপিত শর্ত উল্লেখ করে অবতল দর্পণের ক্ষেত্রে \frac{1}{v}+\frac{1}{u}=\frac{1}{f} সম্পর্কটি প্রতিষ্ঠা কর। এই সূত্র থেকে দেখাও যে, সমতল দর্পণের ক্ষেত্রে প্রতিবিম্বের দূরত্ব = বস্তুর দূরত্ব এবং প্রতিবিম্বটি দর্পণের অপরদিকে গঠিত হয়।
=> 
\overleftrightarrow{PC} হল প্রধান অক্ষ। ফোকাস দূরত্ব=PF=f, বক্রতা ব্যাসার্ধ=PC=r=2f, বস্তু=BA, বস্তু দূরত্ব=PB=u।
A থেকে নির্গত প্রধান অক্ষের সমান্তরাল AR রশ্মি দর্পণ দ্বারা প্রতিফলিত গয়ে F দিয়ে যায়। A থেকে নির্গত C বিন্দুগামী রশ্মি দর্পণ দ্বারা প্রতিফলিত হয়ে আগের পথে গমন করে। রশ্মিদ্বয় পরস্পরকে A’ বিন্দুতে ছেদ করে। A’ থেকে প্রধান অক্ষের উপর অঙ্কিত লম্ব A’B’ হল AB বস্তুর প্রতিবিম্ব।
প্রতিবিম্ব=B’A’, প্রতিবিম্বের দূরত্ব=PB’=v
RS\ \bot PC
চিত্র অনুযায়ী, \Delta CAB\ \sim \Delta CA^\prime B^\prime
\therefore\ \frac{AB}{A^\prime B^\prime} =\frac{BC}{B^\prime C}=\frac{PC-PB}{PB^\prime-PC} (1)
আবার, \Delta FRS\sim\Delta FA^\prime B^\prime
\therefore \frac{RS}{A^\prime B^\prime}= \frac{SF}{B^\prime F}\approx\frac{PF}{B^\prime F} [∵ RA উপাক্ষীয় রশ্মি তাই P ও S বিন্দু কাছাছি অবস্থিত]
or, \frac{AB}{A^\prime B^\prime} = \frac{PF}{B^\prime F} [∵RS=AB]
or, \frac{AB}{A^\prime B^\prime} = \frac{PF}{PB\prime-PF} (2)
(1) ও (2) তুলনা করে পাই
\frac{PC-PB}{PB^\prime-PC}=\frac{PF}{PB\prime-PF}
or, \frac{-2f-(-u)}{-v-(-2f)}=\frac{-f}{-v-(-f)} [চিহ্নের নিয়ম অনুযায়ী]
or, \frac{-2f+u}{-v+2f}=\frac{-f}{-v+f}
or, 2vf-2f^2-uv+uf=vf-2f^2
or, uf+vf=uv
or, \frac{1}{v}+\frac{1}{u}=\frac{1}{f} (3) [উভয়পাশে uvf দিয়ে ভাগ করে পাই]
◊ সমতল দর্পণের ক্ষেত্রে f=∞।
(3) নং সমীকরণে f এর মান বসিয়ে পাই u=-v। অর্থাৎ প্রতিবিম্বের দূরত্ব = বস্তুর দূরত্ব। ঋণাত্মক চিহ্ন বোঝানো হচ্ছে প্রতিবিম্ব দর্পণের অপরদিকে রয়েছে।
3.3 গোলীয় দর্পণের সমীকরণ থেকে দেখাও- a) উত্তল দর্পণ সর্বদা অসদ্ ও ছোট প্রতিবিম্ব গঠন করে। b) অবতল দর্পণে অসদ্ প্রতিবিম্বের বিবর্ধন \frac{v+f}{f} [প্রতীকগুলি প্রচলিত অর্থ বহন করে]
=> a)  উত্তল দর্পণের ক্ষেত্রে সমীকরণ \frac{1}{+v}+\frac{1}{-u}=\frac{1}{+f}
উত্তল দর্পণের ক্ষেত্রে সমীকরণ \frac{1}{+v}+\frac{1}{-u}=\frac{1}{+f}
or, \frac{u}{v}-1=\frac{u}{f}
or, \frac{1}{m}=\frac{u}{f}+1>1
or, m<1
কিন্তু, m=\frac{ প্রতিবিম্বের\; দৈর্ঘ্য}{ বস্তুর\; দৈর্ঘ্য}
∴\frac{ প্রতিবিম্বের\; দৈর্ঘ্য}{ বস্তুর\; দৈর্ঘ্য}<1
or, প্রতিবিম্বের দৈর্ঘ্য<বস্তুর দৈর্ঘ্য

b) অবতল দর্পণের ক্ষেত্রে সমীকরণ \frac{1}{+v}+\frac{1}{-u}=\frac{1}{-f}
or, \frac{1}{v}-\frac{1}{u}=-\frac{1}{f}
or, 1-m=\frac{v}{f}
or,m=\frac{v}{f}+1=\frac{v+f}{f}
3.4 দেখাও যে গোলীয় দর্পণ দ্বারা সৃষ্ট প্রতিবিম্বের রৈখিক বিবর্ধন=\frac{প্রতিবিম্বের \;দূরত্ব}{ বস্তু \;দূরত্ব}=\frac{ প্রতিবিম্বের\; দৈর্ঘ্য}{ বস্তুর \; দৈর্ঘ্য}
=>  পাশের চিত্রে, AB বস্তুর প্রতিবিম্ব A'B'। মেরু P থেকে বস্তু ও প্রতিবিম্বের দূরত্ব যথাক্রমে PB =u ও PB'=v।বস্তু ও প্রতিবিম্বের দৈর্ঘ্যর যথাক্রমে O ও I।
পাশের চিত্রে, AB বস্তুর প্রতিবিম্ব A'B'। মেরু P থেকে বস্তু ও প্রতিবিম্বের দূরত্ব যথাক্রমে PB =u ও PB'=v।বস্তু ও প্রতিবিম্বের দৈর্ঘ্যর যথাক্রমে O ও I।
\Delta PAB \sim\Delta PA^\prime B^\prime
\therefore\ \frac{A\prime B\prime}{AB}=\frac{PB\prime}{PB}
or, \frac{-I}{O}=\frac{-v}{-u}
or, m=\frac{I}{O}=-\frac{v}{u}
3.5 একটি গোলীয় দর্পণের সম্মুখে u দূরত্বে b দৈর্ঘ্যের একটি ক্ষুদ্র বস্তুকে প্রধান অক্ষের সঙ্গে সমান্তরালে রাখা হল। প্রমাণ কর, প্রতিবিম্বের দৈর্ঘ্য = b{(\frac{f}{u-f})}^2, যেখানে f= দর্পণের ফোকাস দৈর্ঘ্য।
=> u = বস্তুর অগ্রভাগের দূরত্ব  , v= প্রতিবিম্বের অগ্রভাগের দূরত্ব
, v= প্রতিবিম্বের অগ্রভাগের দূরত্ব
∴ \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{v}=\frac{1}{f}-\frac{1}{u}
or, v=\frac{uf}{u-f}
এখন, বস্তুর পশ্চাদভাগের দূরত্ব = u_1 =u+b, প্রতিবিম্বের পশ্চাদভাগের =v_1 হলে,
\frac{1}{v_1}+\frac{1}{u_1}=\frac{1}{f}
or, \frac{1}{v_1}=\frac{1}{f}-\frac{1}{u_1}
or, \frac{1}{v_1}=\frac{1}{f}-\frac{1}{u+b} = \frac{u+b-f}{(u+b)f}
or, v_1= \frac{(u+b)f}{u+b-f}
প্রতিবিম্বের দৈর্ঘ্য= v_1-v = \frac{u+b-f}{(u+b)f}-\frac{(u+b)f}{u+b-f}
= \frac{(u + b)(u - f) - u(u + b - f)}{(u - f)(u + b - f)}\ldotp f
= \frac{\cancel{u^2} - \cancel{uf} + \cancel{ub} - bf - \cancel{u^2} - \cancel{ub} + \cancel{bf}}{{(u - f)(u + b - f)}}\ldotp f
= - \frac{bf}{(u - f)^2} [\because b ক্ষুদ্র]
3.6 একটি অবতল দর্পণের ফোকাসে বস্তু রাখলে তার প্রতিবিম্বের গঠন রশ্মিচিত্রের সাহায্যে দেখাও।
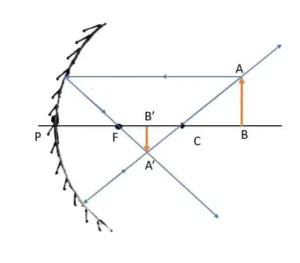
=>  অবতল দর্পণের ফোকাস F-এ AF বস্ত রয়েছে। A থেকে প্রধান অক্ষের সমান্তরাল একটি রশ্মি দর্পণ থেকে প্রতিফলিত হয়ে ফোকাস দিয়ে যায়। A থেকে নির্গত বক্রতাকেন্দ্রগামী (C) রশ্মি দর্পণ থেকে প্রতিফলিত হয়ে আগের পথেই ফিরে যায়। A বিন্দু থেকে নেওয়া রশ্মি দুটি প্রতিফলিত রশ্মি দুটি সমান্তরাল হয়।
অবতল দর্পণের ফোকাস F-এ AF বস্ত রয়েছে। A থেকে প্রধান অক্ষের সমান্তরাল একটি রশ্মি দর্পণ থেকে প্রতিফলিত হয়ে ফোকাস দিয়ে যায়। A থেকে নির্গত বক্রতাকেন্দ্রগামী (C) রশ্মি দর্পণ থেকে প্রতিফলিত হয়ে আগের পথেই ফিরে যায়। A বিন্দু থেকে নেওয়া রশ্মি দুটি প্রতিফলিত রশ্মি দুটি সমান্তরাল হয়।
প্রতিবম্বটি অসীমে তৈরি হবে যা সদ্ ও আকারে অসীমভাবে বিবর্ধিত।
3.7 দর্পণের সূত্র থেকে দেখাও যে যখন একটি বস্তুকে একটি অবতল দর্পণের মেরু ও ফোকাসের মধ্যে রাখা হয় তখন দর্পণটি বস্তুর বিবর্ধিত, অসদ্ এবং সমশীর্ষ প্রতিবিম্ব গঠন করে।
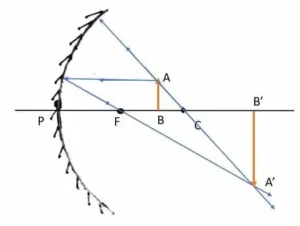
=> চিত্রে AB বস্তুর প্রতিবিম্ব A'B'। u<f
ধরি, u=(f-x) [x<f]
চিহ্নের নিয়ম অনুযায়ী
\frac{1}{v}-\frac{1}{f-x}=-\frac{1}{f}
or, \frac{1}{v}=\frac{1}{f-x}-\frac{1}{f}
or, \frac{1}{v}=\frac{x}{(f-x)f}
or, v=\frac{f(f-x)}{x}
সুতরাং, v হল +ve। এর অর্থ হল প্রতিবিম্ব অসদ্ মানে দর্পণের পিছনে এবং সমশীর্ষ হবে।
বিবর্ধন, m=\frac{v}{u}=\frac{f}{x} [যেহেতু, u=f-x]
or, m>1 [যেহেতু, f>x]
∴ প্রতিবিম্ব আকারে বড় হবে।
4. গোলীয় তলে আলোর প্রতিফলন-গাণিতিক প্রশ্নোত্তর (Marks-2/3)
গোলীয় তলে আলোর প্রতিফলন
4.1 একটি অভিসারী রশ্মিগুচ্ছ 20 cm বক্রতা ব্যাসার্ধের একটি উত্তল দর্পণে প্রতিফলিত হওয়ার পর দর্পণের 15 cm সামনে মিলিত হল। দর্পণটি না থাকলে রশ্মিগুচ্ছ কোথায় মিলিত হত?
=>r= 20 cm সুতরাং f= 10 cm
v= 15 cm
দর্পণের সমীকরণ অনুযায়ী, \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{-15}+\frac{1}{u}=\frac{1}{10} [চিহ্নের নিয়ম ব্যবহার করে]
or, \frac{1}{u}=\frac{1}{10}+\frac{1}{15}
or, u=6
দর্পণ না থাকলে 6 মিটার পিছনে অভিসারী রশ্মিগুলি মিলিত হতো।
4.2 f ফোকাস দৈর্ঘ্যের একটি অবতল দর্পণের সামনে 2.5 cm দীর্ঘ একটি বস্তু প্রধান অক্ষের সঙ্গে লম্বভাবে \frac{3}{4}f দূরত্বে রাখা হলে বস্তুর দূরত্বে রাখা বস্তুর প্রতিবিম্বের প্রকৃতি কীরূপ হবে? প্রতিবিম্বের দৈর্ঘ্য কত হবে?
=>বস্তুর দৈর্ঘ্য (x) = 2.5cm, u = \frac{3f}{4}
দর্পণের সমীকরণ, \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{v}+\frac{-4}{3f}=\frac{1}{-f} [চিহ্নের নিয়ম ব্যবহার করে
or, \frac{1}{v}=-\frac{1}{f}+\frac{4}{3f}=\frac{1}{3f}
or, v=3f [প্রতিবিম্ব অসদ্]
বিবর্ধন (m)=-\frac{v}{u}=-\frac{3f}{\frac{-3f}{4}}=4
আবার, m = \frac{y}{x} [y=প্রতিবিম্বের দৈর্ঘ্য]
or, \frac{y}{2.5}=4
or, y= 10 cm
4.3 একটি বস্তুকে একটি উত্তল দর্পণ থেকে 60 cm দূরে রাখা হল। প্রতিবিম্বের দৈর্ঘ্য বস্তুর দৈর্ঘ্যের এক-তৃতীয়াংশ। দর্পণের বক্রতা ব্যাসার্ধকত?
=> u= 60 cm
প্রতিবিম্বের দৈর্ঘ্য (y) = বস্তুর দৈর্ঘ্য (x)×1/3
or, \frac{y}{x}=\frac{1}{3}
or, \frac{v}{u}=\frac{1}{3}
or, v=\frac{u}{3}=\frac{60}{3} cm = 20 cm
দর্পণের সমীকরণ, \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{20}-\frac{1}{60}=\frac{1}{f} [উত্তল দর্পণের চিহ্নের নিয়ম ব্যবহার করে]
or, \frac{1}{f}=\frac{1}{30} or, f=30 or, r=2f= 60 cm
4.4 একটি বস্তুকে 40 cm বক্রতা ব্যাসার্ধের একটি অবতল দর্পণ ও 30 cm বক্রতা ব্যাসার্ধের একটি উত্তল দর্পণের ঠিক মাঝখানে রাখ হল। দর্পণ দুটি পরস্পরের মুখোমুখি ও একে অপর থেকে 50 cm দূরত্বে অবস্থিত। প্রথমে অবতল দর্পণে গঠিত বস্তুটির প্রতিবিম্বের অবস্থান ও প্রকৃতি নির্ণয় করো এবং তারপর এই প্রতিবিম্বের উত্তল দর্পণে যে প্রতিবিম্ব হবে তার অবস্থান ও প্রকৃতি কী হবে, তা নির্ণয় করো।
=>  অবতল দর্পণের ফোকাস দৈর্ঘ্য (f1) = \frac{40}{2} cm=20 cm
অবতল দর্পণের ফোকাস দৈর্ঘ্য (f1) = \frac{40}{2} cm=20 cm
অবতল দর্পণ থেকে বস্তুর দূরত্ব (u1)= 25 cm
অবতল দর্পণ থেকে প্রতিবিম্বের দূরত্ব= v1
দর্পণের সমীকরণ- \frac{1}{v_1}+\frac{1}{u_1}=\frac{1}{f_1}
or, \frac{1}{v_1}+\frac{1}{u_1}=\frac{1}{f_1} [অবতল দর্পণে চিহ্নের নিয়ম]
or, \frac{1}{v_1}+\frac{1}{-25}=\frac{1}{-20}
or, \frac{1}{v_1}=\frac{1}{25}-\frac{1}{20}= -\frac{1}{100}
∴v1 =-100 cm
অবতল দর্পণ দ্বারা গঠিত প্রতিবিম্বটি (সদ্) দর্পণ থেকে 100 cm দূরে তৈরি হবে।
এই প্রথম প্রতিবিম্ব থেকে উত্তল দর্পণের দূরত্ব (u2)= (100-50) cm= 50 cm
উত্তল দর্পণের ফোকাস দৈর্ঘ্য (f2) = \frac{30}{2} cm=15 cm।
উত্তল দর্পণ দ্বারা গঠিত প্রতিবিম্বের দূরত্ব= v2
দর্পণের সমীকরণ- \frac{1}{v_2}+\frac{1}{u_2}=\frac{1}{f_2}
or, \frac{1}{v_1}+\frac{1}{50}=\frac{1}{15} [অভিসারী রশ্মির ক্ষেত্রে উত্তল দর্পণে চিহ্নের নিয়ম]
or, \frac{1}{v_1}=\frac{1}{15} -\frac{1}{50}=\frac{7}{150}
∴v2=\frac{150}{7} cm= 21.43 cm (প্রায়)
দ্বিতীয় প্রতিবিম্বটি অসদ্ প্রকৃতির হবে।
4.5 একটি ফাঁপা ধাতব গোলকের অভ্যন্তরভাগকে একটি দর্পণ হিসেবে ব্যবহার করতে পালিশ করা হয়। 24 cm ব্যাসার্ধবিশিস্ট গোলকটির কেন্দ্র থেকে 12 cm দূরত্বে একটি বিন্দুতে আলোর একটি বিন্দু উৎস রাখা হয়। পরপর দুটি প্রতিফলনের ফলে এর প্রতিবিম্ব কোথায় গঠিত হবে, তা চিহ্নিত করো। যখন প্রথম প্রতিফলনটি (a) দেয়াল থেকে দূরে, (b) দেয়ালের কাছাকাছি হয়।
=> ধাতব গোলক অবতল দর্পণের মতো আচরণ করবে। এর বক্রতা ব্যাসার্ধ f=\frac{r}{2}=\frac{24}{2} cm 12 cm।
বস্তু S বিন্দুতে অবস্থিত।
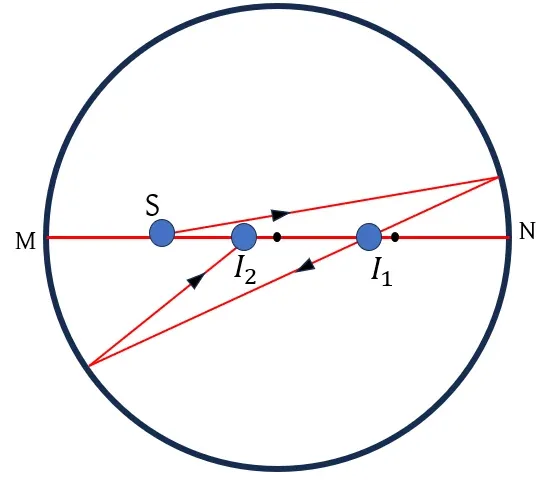
a) প্রথম প্রতিফলনটি যখন দেয়াল থেকে দূরে (N তলে)-
u1 =(24+12) cm =36 cm
∴ \frac{1}{v_1}+\frac{1}{-36}=\frac{1}{-12}
or, \frac{1}{v_1}=\frac{1}{-36}-\frac{1}{12} = -\frac{1}{18}
∴ v1=-18 cm।
প্রথম প্রতিবিম্ব তৈরি হবে I1 বিন্দুতে। I1N=18 cm।
I1 থেকে নির্গত রশ্মি M তলে প্রতিফলিত হবে।
এখন u2 = MN- I1N = (2×24-18) cm =30 cm।
∴ \frac{1}{v_2}+\frac{1}{-30}=\frac{1}{-12}
or, \frac{1}{v_2}\frac{1}{30}-\frac{1}{12} = -\frac{1}{20}
∴ v2=-20 cm।
অন্তিম প্রতিবিম্ব (I2) M প্রান্ত থেকে 20 cm দূরে তৈরি হবে।

b) প্রথম প্রতিফলনটি যখন দেয়াল থেকে দূরে (M তলে)-
এক্ষেত্রে বস্তুর অবস্থান M তলের ফোকাস। তাই এখান থেকে নির্গত রশ্মি M তলে প্রতিফলিত হয়ে প্রধান অক্ষের সমান্তরাল হবে। N তলে এই রশ্মি আবার প্রতিফলিত হয়ে N তলের ফোকাসে মিলিত হবে। অর্থাৎ N থেকে 12 cm দূরে।
4.6 1m বক্রতা ব্যাসার্ধবিশিষ্ট একটি অবতল দর্পণের মেরু থেকে 75 cm দূরত্বে প্রধান অক্ষের ওপর একটি স্বপ্রভ বিন্দু উৎস P-কে রাখা হল। অবতল দর্পণ থেকে কত দূরত্বে একটি সমতল দর্পণ রাখা হলে, P বিন্দু থেকে আগত রশ্মিগুচ্ছ প্রথমে অবতল ও পরে সমতল দর্পণে প্রতিফলিত হওয়ার পর আবার P বিন্দুতে মিলিত হবে? যদি P থেকে আগত রশ্মি প্রথমে সমতল দর্পণ এবং তারপর অবতল দর্পণে প্রতিফলিত হয় তাহলে রশ্মির অভিসরণ বিন্দুর অবস্থান পরিবর্তন হবে কি?
=> 
u= -75 cm, f=\frac{r}{2}= -\frac{1}{2} m=- 50 cm
অবতল দর্পণ দ্বারা উৎপন্ন P বিন্দুর প্রতিবিম্ব P' এর দূরত্ব (OP') =v।
∴ \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{v}+\frac{1}{-75}=\frac{1}{-50}
or, \frac{1}{v}=-\frac{1}{50}+\frac{1}{75}=-\frac{1}{150}
or, v=-150
PP'=OP'-OP=(150-75) cm =75 cm
সমতল দর্পণে, বস্তুর দূরত্ব= প্রতিবিম্বের দূরত্ব
তাই, সমতল দর্পণ থেকে প্রতিবিম্বের দূরত্ব= \frac{75}{2} cm =37.5 cm
∴ অবতল দর্পণ ও প্রতিবিম্বের দূরত্ব= OP+37.5 cm =(75 +37.5) cm =112.5 cm
♦ যদি P থেকে আগত রশ্মি প্রথমে সমতল দর্পণ এবং তারপর অবতল দর্পণে প্রতিফলিত হয় তাহলে রশ্মির অভিসরণ বিন্দুর অবস্থান পরিবর্তন হবে না।
4.7 একটি সমতল দর্পণ 1.5 cm পুরু কাচের তৈরি। তার পিছনের দিকে পারদ প্রলেপিত আছে। দর্পণের সামনে দর্পণ থেকে 50 cm দূরে দাঁড়ানো কোনো ব্যক্তি তাতে লম্বভাবে তাকালে তার প্রতিবিম্ব দর্পণের সামনের তল থেকে কত দূরে যাবে? (কাচের প্রতিসরাঙ্ক μ=1.5)
=>

পুরু কাচের আপাত গভীরতা d'=\frac{d}{\mu}=\frac{1.5}{1.5} cm= 1 cm
ব্যক্তি থেকে পুরু কাচের আপাত দূরত্ব x=(50+1) cm = 51 cm
এই আপাত তল থেকে ব্যক্তির প্রতিবিম্বের দূরত্ব হবে= 51 cm
∴ প্রতিবিম্ব থেকে কাচের মসৃন তলের দূরত্ব 51 cm+d'= (51+1) cm= 52 cm
4.8 70 cm বক্রতা ব্যাসার্ধবিশিষ্ট একটি উত্তল দর্পণ এবং একটি সমতল দর্পণকে পরস্পরের মুখোমুখিভাবে রাখা হল। তাদের দূরত্ব 28 cm। দর্পণের প্রধান অক্ষের ওপর একটি বিন্দু বস্তুকে উত্তল দর্পণ ও সমতল দর্পণের মধ্যবিন্দুতে রাখা হল। বস্তুর দুটি প্রতিবিম্ব সমতল দর্পণে দেখতে পাওয়া গেল। সমতল দর্পণ থেকে এদের দূরত্ব নির্ণয় করো।
=> 
উত্তল দর্পণের ফোকাস দৈর্ঘ্য f=+\frac{70}{2} cm =35 cm
উত্তল দর্পণ ও সমতল দর্পণের মধ্যে দূরত্ব O1O2=28 cm
উত্তল দর্পণ ও বস্তুর দূরত্ব (O1P)=u = \frac{O_1O_2}{2}=-\frac{28}{2} cm =-14 cm
উত্তল দর্পণ ও প্রতিবিম্বের দূরত্ব O1P'=v
∴ \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{v}+\frac{1}{-14}=\frac{1}{35}
or, \frac{1}{v}=\frac{1}{35}+\frac{1}{14}=\frac{1}{10}
or, v=10 cm সুতরাং প্রতিবিম্বটি অসদ্ হবে।
এবার সমতল দর্পণ থেকে P' প্রতিবিম্বের দূরত্ব P'O2=P'O1+O1O2= (10+28) cm=38 cm
এখন P'-কে বস্তু হিসেবে কল্পনা করে সমতল দর্পণের অভ্যন্তরে P'' প্রতিবিম্ব তৈরি হবে। ∴ O2P''=P'O2= 38 cm
অন্যদিকে, P এর একটি প্রতিবিম্ব সমতল দর্পণের তৈরি হবে P1 বিন্দুতে। সমতল দর্পণ থেকে এর দূরত্ব হবে O2P1=O2P= 14 cm [∵ P দুই দর্পণের মাঝে অবস্থিত]
4.9 একটি অবতল দর্পণের সম্মুখে 50 cm দূরত্বে অবস্থিত একটি বস্তুর প্রতিবিম্ব দর্পণটির পিছনে 2m দূরত্বে গঠিত হয়। দর্পণটির ফোকাস দূরত্ব ও বক্রতা ব্যাসার্ধ কত?
=> u=-50 cm, v= +2 m =+200 cm
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{f}=\frac{1}{200}+\frac{1}{-50}=\frac{-3}{200}
or, f=-\frac{200}{3} cm=-66.67 cm
r=2f=-2×66.67 cm = -133.33 cm
4.10 একটি অবতল দর্পণ দ্বারা গঠিত প্রতিবিম্বের আকার বস্তুর আকারের এক-চতুর্থাংশ হয়। যদি বস্তুটিকে দর্পণের দিকে 10 cm সরানো হয় তাহলে এর প্রতিবিম্বটি এর আকারের অর্ধেক হয়। দর্পণের ফোকাস দৈর্ঘ্য নির্ণয় করো।
=> -\frac{v_1}{u_1}=\frac{1}{4} or, v_1=-\frac{u_1}{4}
\frac{1}{v_1}+\frac{1}{u_1}=\frac{1}{f}
or, \frac{-4}{u_1}+\frac{1}{u_1}=\frac{1}{f}
or, -\frac{3}{u_1}=\frac{1}{f}
or, u_1=-3f
আবার, -\frac{v_2}{u_2}=\frac{1}{2} or, v_2=-\frac{u_2}{2}
\frac{1}{v_2}+\frac{1}{u_2}=\frac{1}{f}
or, \frac{-2}{u_2}+\frac{1}{u_2}=\frac{1}{f}
or, -\frac{1}{u_2}=\frac{1}{f}
or, u_2=-f
u_1-u_2=-3f+f=-2f
or, 10=-2f
or, f=-5 cm
4.11 একটি উত্তল দর্পণে একটি বস্তুর 1/n গুণ আকারের প্রতিবিম্ব গঠিত হয়। দর্পণের বক্রতা ব্যাসার্ধ। হলে, বস্তুদূরত্ব কত?
=> উত্তল দর্পণের সমীকরণ
\frac{1}{v}+\frac{1}{-u}=\frac{1}{f}=\frac{2}{r}
or, \frac{u}{v}-1=\frac{2u}{r}
or, n-1=\frac{2u}{r} [∵ \frac{v}{u}=\frac{1}{n}]
or, u=\frac{(n-1)r}{2}
4.12 গোলীয় দর্পণের সাহায্যে একটি বস্তুর তিনগুণ বিবর্ধিত প্রতিবিম্ব বস্তু থেকে ৪ cm দূরে পর্দায় গঠিত হয়। দর্পণের প্রকৃতি, ফোকাস দূরত্ব এবং বস্তু থেকে দর্পণটির দূরত্ব নির্ণয় করো।
=> \left|\frac{v}{u}\right|=3 or, v=3u
v-u=8
or, 3u-u=8
or, 2u=8
∴ u=4 cm
প্রতিবিম্ব পর্দায় তৈরি হয়েছে মানে সদ্বিম্ব এবং দর্পণটি অবতল।
v=3×4 cm=12 cm
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{-12}+\frac{1}{-4}=\frac{1}{f} [অবতল দর্পণে চিহ্নের নিয়ম]
or, \frac{1}{f}=\frac{-1}{3}
∴ f=-3 cm
4.13 উত্তল দর্পণ থেকে 10 cm দূরে অক্ষের ওপর 5 cm দীর্ঘ একটি বস্তু অবস্থিত। দর্পণের ফোকাস দূরত্ব 20 cm। প্রতিবিম্বের অবস্থান, প্রকৃতি ও দৈর্ঘ্য নির্ণয় করো।
=> u=-10 cm
বস্তুর দৈর্ঘ্য (x) = 5 cm
f= 20 cm
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{v}+\frac{1}{-10}=\frac{1}{20}
or, \frac{1}{v}=\frac{1}{20}+\frac{1}{10}=\frac{3}{20}
or, v=\frac{20}{3}= 6.67 cm
বিবর্ধন= -\frac{v}{u}=-frac{\frac{20}{3}}{-5}=\frac{2}{3}
প্রতিবিম্বের দৈর্ঘ্য y হলে
\frac{y}{x}=\frac{2}{3}
or, \frac{y}{5}=\frac{2}{3}
or, y=\frac{10}{3}=3.33 cm
4.14 একটি অভিসারী রশ্মিগুচ্ছ 30 cm ফোকাস দৈর্ঘ্যবিশিষ্ট একটি উত্তল দর্পণে আপতিত হল। এর অনুপস্থিতিতে রশ্মিগুচ্ছ দর্পণের মেবু থেকে 20 cm দূরে মিলিত হতো। উক্ত স্থানে দর্পণটি অবস্থিত হলে, রশ্মিগুচ্ছ প্রকৃতপক্ষে কোথায় মিলিত হবে?
=> অভিসারী রশ্মির ক্ষেত্রে u=20cm, f= 30 cm>
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{v}+\frac{1}{20}=\frac{1}{30}
or, \frac{1}{v}=\frac{1}{30}-\frac{1}{20}=-\frac{1}{60}
∴ v=-60 cm
দর্পণের সামনে 60 cm দূরে তৈরি হবে।
4.15 যখন একটি বস্তুকে একটি উত্তল দর্পণ থেকে 60 mm দূরে রাখা হয়, তখন তার বিবর্ধন হয় 1/2 বস্তুটিকে কোথায় রাখলে তার বিবর্ধন 1/3 হবে?
=> u= -60 mm, -\frac{v}{u}=\frac{1}{2} or, v=-\frac{u}{2}= -\frac{-60}{2} mm=30 mm
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{30}+\frac{1}{60}=\frac{1}{f}
or, \frac{1}{f}=\frac{1}{60} cm
∴ f=60 mm
আবার, -\frac{v}{u}=\frac{1}{3}
এখন, \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{u}{v}+1=\frac{u}{f}
or, -3+1=\frac{u}{f}
u=-2×60 mm= -120 mm
4.16 একটি অবতল দর্পণের সামনে 22.5 cm দূরে একটি সমতল দর্পণ রাখা আছে। অবতল দর্পণের ফোকাস দূরত্ব 10 cm। কোনো একটি বস্তুকে দুটি দর্পণের মাঝে কোথায় রাখলে প্রথম দুটি প্রতিবিম্ব সমাপতিত হবে?
=> 
f= -10 cm. O1O2= 22.5 cm
ধরি, অবতল দর্পণ (O2) থেকে x দূরত্বে P বিন্দুতে বস্তুকে রাখলে দর্পণ দুটির প্রতবিম্ব একই বিন্দুতে সমাপতিত হবে।
∴ PO2=O1O2-O1P=(22.5-x) cm
সমতল দর্পণের জন্য দর্পণের অভ্যন্তরে P1 বিন্দুতে প্রতিবিম্ব তৈরি হলে O2P1= PO2=(22.5-x) cm [∵ সমতল দর্পণে, বস্তু দূরত্ব= প্রতিবিম্ব দূরত্ব]
প্রশ্নানুযায়ী, অবতল দর্পণের জন্য প্রতিবিম্বটিও P1 বিন্দুতে তৈরি হবে।
∴ অবতল দর্পণের v= O1P1= O1O2+O2P1= (22.5+22.5-x) cm= (45-x) cm
∴ \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{-(45-x)}+\frac{1}{-x}=\frac{1}{-10} [চিহ্নের নিয়ম]
or, \frac{x+45-x}{(45-x)x}=\frac{1}{10}
or, 450 = 45x-x^2
or, x^2-45x+450=0
or, x=\frac{45 \pm \sqrt{45^2-4 \times 1 \times 450}}{2}
or, x=\frac{45 \pm 15}{2} = 30, 15
x= 30 অগ্রাহ্য হবে কারণ অবতল দর্পণ থেকে বস্তু দূরত্ব x<O1O2 হবে।
∴ x= 15 cm
4.17 চাঁদের ব্যাস 3450 km এবং পৃথিবী থেকে চাঁদের দূরত্ব 3.8×105 km। যে অবতল দর্পণের ফোকাস দৈর্ঘ্য 7.6 m, তার দ্বারা গঠিত চাঁদের প্রতিবিম্বের ব্যাস কত হবে?
=>
চাঁদের ব্যাসার্ধ (H) \frac{3450}{2} km = 1725 km
অবতল দর্পণের f= 7.6 m
পৃথিবী থেকে চাঁদের দূরত্ব , X= 3.8×105 km
চাঁদ থেকে আগত আলোক রশ্মি অবতল দর্পণের ফোকাসে θ কোণ তৈরি করলে \frac{H}{X}=tan \theta
or, tan\theta=\frac{1725}{3.8 \times 10^5} rad= 4.5×10-3 rad
চাঁদের প্রতিবিম্বের ব্যাসার্ধ h হলে \frac{h}{f}=tan \theta
or, h=4.5×10-3×7.6 m= 0.0342 m = 3.42 cm
প্রতিবিম্বের ব্যাস 2×3.42 cm = 6.84 cm

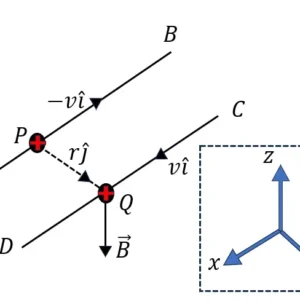

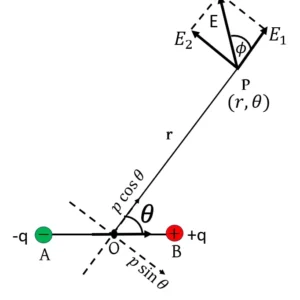


 ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠