1. তড়িৎ দ্বিমেরুর অক্ষের উপর অবস্থিত কোনো বিন্দুতে তড়িৎক্ষেত্র নির্ণয়-

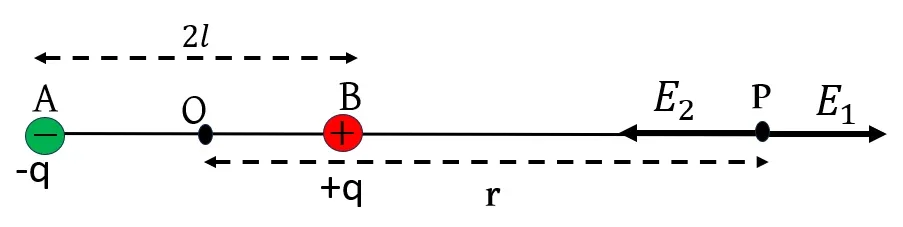
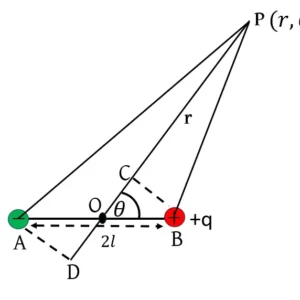
ধরি, কোনো তড়িৎ দ্বিমেরু ধনাত্মক ও ঋণাত্মক আধানের মান যথাক্রমে +q ও -q। এদের মধ্যে দূরত্ব 2\vec{l} হলে তড়িৎ দ্বিমেরু p=2l\times q=2ql। তড়িৎদ্বিমেরুর মধ্যবিন্দু O থেকে অক্ষ বরাবর r দূরত্বে P বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য (E) নির্ণয় করতে হবে।

+q আধানের জন্য P বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য, E_1=\frac{1}{4\pi\varepsilon_0}\frac{q}{\left(r-l\right)^2}  (\overrightarrow{OP} বরাবর)
-q আধানের জন্য P বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য, E_2=\frac{1}{4\pi\varepsilon_0}\frac{q}{\left(r+l\right)^2}  (\overrightarrow{PO} বরাবর)
+q আধান; -q আধানের তুলনায় P বিন্দুর কাছে অবস্থান করায় E_1>E_2 হবে।

P বিন্দুতে লব্ধি তড়িৎ ক্ষেত্রপ্রাবল্য E=E_1-E_2    (\overrightarrow{OP} বরাবর)

= \frac{1}{4\pi\varepsilon_0}\frac{q}{\left(r-l\right)^2}-\frac{1}{4\pi\varepsilon_0}\frac{q}{\left(r+l\right)^2}
 = \frac{q}{4\pi\varepsilon_0}(\frac{1}{\left(r-l\right)^2}-\frac{1}{\left(r+l\right)^2})
= \frac{q}{4\pi\varepsilon_0}[\frac{\left(r+l\right)^2-\left(r-l\right)^2}{\left(r-l\right)^2\left(r+l\right)^2}]
= \frac{q}{4\pi\varepsilon_0}\frac{4rl}{\left(r^2-l^2\right)^2}

∴ E=\frac{1}{4\pi\varepsilon_0}\frac{2pr}{\left(r^2-l^2\right)^2}               [∵p=2ql] 

r>>l হলে \left(r^2-l^2\right)^2\approx r^4

∴ E=\frac{1}{4\pi\varepsilon_0}\frac{2pr}{r^4}
\;\;\;\;\;=\frac{1}{4\pi\varepsilon_0}\frac{2p}{r^3}

2. তড়িৎ দ্বিমেরুর লম্বসমদ্বিখন্ডকের উপরিস্থিত কোনো বিন্দুতে তড়িৎক্ষেত্র নির্ণয়

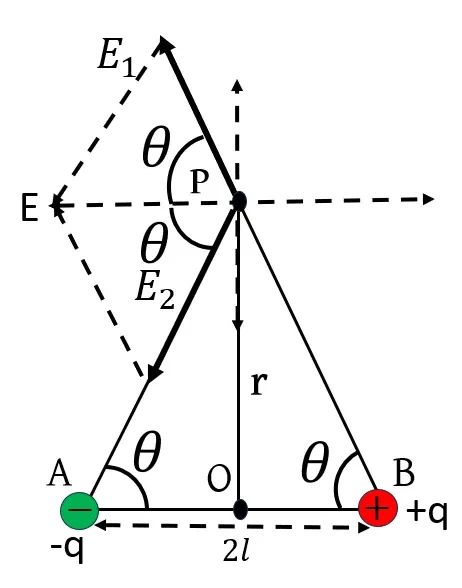
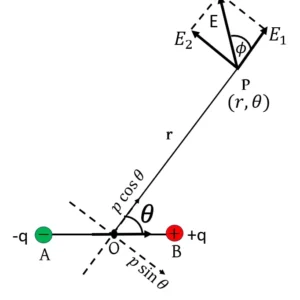
ধরি, কোনো তড়িৎ দ্বিমেরু ধনাত্মক ও ঋণাত্মক আধানের মান যথাক্রমে +q ও -q। এদের মধ্যে দূরত্ব 2\vec{l} হলে তড়িৎ দ্বিমেরু p=2l\times q=2ql। তড়িৎ দ্বিমেরুর মধ্যবিন্দু O থেকে লম্ব অক্ষ বরাবর r দূরত্বে P বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য (E) নির্ণয় করতে হবে।

+q আধানের জন্য P বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য, E_1=\frac{1}{4\pi\varepsilon_0}\frac{q}{\left(r^2+l^2\right)}  (\overrightarrow{BP} বরাবর)
-q আধানের জন্য P বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য, E_2=\frac{1}{4\pi\varepsilon_0}\frac{q}{\left(r^2+l^2\right)}  (\overrightarrow{PA} বরাবর)

এখন, E_1=E_2=\frac{1}{4\pi\varepsilon_0}\frac{q}{\left(r^2+l^2\right)}=k (ধরি) এবং এদের মধ্যবর্তী কোণ 2θ।

এদের লব্ধি, E=\sqrt{E_1^2+E_2^2+2.E_1.E_2.cos2\theta}
=\sqrt{k^2+k^2+2.k.k.cos2\theta}
=k\sqrt{2\left(1+cos2\theta\right)}
=k\sqrt{2.2cos^2\theta}
=2kcos\theta=2. \frac{1}{4\pi\varepsilon_0}\frac{q}{\left(r^2+l^2\right)}.\frac{l}{\sqrt{r^2+l^2}}
=\frac{1}{4\pi\varepsilon_0}.\frac{2ql}{\left(r^2+l^2\right)^{3/2}}
=\frac{1}{4\pi\varepsilon_0}.\frac{p}{\left(r^2+l^2\right)^{3/2}}

∴E=\frac{1}{4\pi\varepsilon_0}.\frac{p}{\left(r^2+l^2\right)^{3/2}}

E_1 ও E-এর মধ্যবর্তী কোণ \phi  হলে, tan\phi=\frac{E_2sin2\theta}{E_1+E_2cos2\theta}

or, tan\phi=\frac{ksin2\theta}{k+kcos2\theta}
=\frac{sin2\theta}{1+cos2\theta}
=\frac{2sin\theta.cos\theta}{2cos^2\theta}=tanθ

\therefore\phi=\theta

লব্ধি তড়িৎক্ষেত্র প্রাবল্য E তড়িৎ দ্বিমেরুর অক্ষের সমান্তরালে \overrightarrow{BA} বরাবর ক্রিয়া করবে।

r>>l হলে \left(r^2+l^2\right)^{3/2}\approx r^3

\therefore E=\frac{1}{4\pi\varepsilon_0}\frac{p}{r^3}

3. তড়িৎ দ্বিমেরুর জন্য যেকোনো বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য নির্ণয়

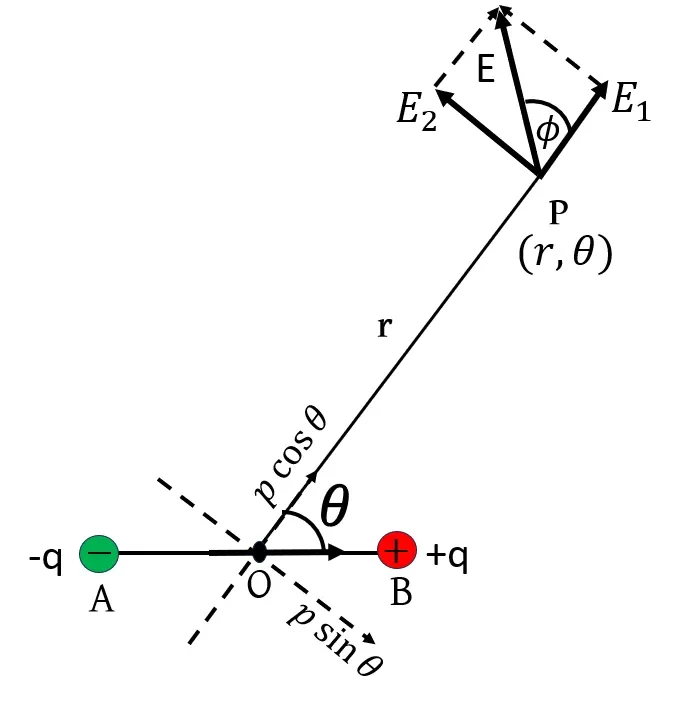
তড়িৎদ্বিমেরুর মধ্যবিন্দু O-কে মূলবিন্দু ভেবে P(r,θ) বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য নির্ণয় করতে হবে।

OP বরাবর p তড়িৎদ্বিমেরুর উপাংশ p\cos{\theta}

OP-এর লম্ব বরাবর p তড়িৎ দ্বিমেরুর উপাংশ psin{\theta}

p\cos{\theta}-এর জন্য P বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য
 E_1=\frac{1}{4\pi\varepsilon_0}\frac{2pcos{\theta}}{r^3}

p\sin{\theta}-এর জন্য P বিন্দুতে তড়িৎক্ষেত্র প্রাবল্য
E_2=\frac{1}{4\pi\varepsilon_0}\frac{psin{\theta}}{r^3}

কিন্তু E_1\bot E_2

সুতরাং এদের লব্ধি, E=\sqrt{E_1^2+E_2^2}

=\sqrt{\left(\frac{1}{4\pi\varepsilon_0}\frac{2pcos{\theta}}{r^3}\right)^2+\left(\frac{1}{4\pi\varepsilon_0}\frac{psin{\theta}}{r^3}\right)^2}
=\frac{p}{4\pi\varepsilon_0r^3}\sqrt{\left(2cos\theta\right)^2+\left(sin\theta\right)^2}
=\frac{p}{4\pi\varepsilon_0r^3}\sqrt{4cos^2\theta+sin^2\theta}

∴E=\frac{p}{4\pi\varepsilon_0 r^3}\sqrt{3cos^2{\theta}+1}

অন্যান্য লিংক

তড়িৎ বলরেখান সম্পর্কে জানতে এখানে ক্লিক করুন।

CLASS XII PHYSCIS