তড়িৎচুম্বক অধ্যায়:প্রশ্নোত্তর
দুটি প্রোটন x অক্ষের সমান্তরালে পরস্পরের বিপরীতে v বেগে (<< c, শূন্যমাধ্যমে আলোর বেগ) চলছে। যে-কোনো একটি সময়ে চৌম্বক বল ও তড়িৎ বলের অনুপাত হবে-
A) \frac{v}{c} B) \frac{v^2}{c^2} C) \frac{v^3}{c^3} D) \sqrt{\frac{v}{c}}
উত্তর-
প্রথমে জেনে নেই আধান প্রবাহের জন্য বায়ো-সাভার্ট সূত্র।
আমরা জানি, d\vec{B}=\frac{\mu_0}{4\pi}\frac{Id\vec{l}\times \vec{r}}{r^3} [চিহ্নগুলি প্রচলিত অর্থ বহন করে]
\;\;\;\;\;=\frac{\mu_0}{4\pi}\frac{dq}{dt}\frac{d\vec{l}\times \vec{r}}{r^3}
\;\;\;\;\;=\frac{\mu_0}{4\pi}dq.\frac{d\vec{l}}{dt}\times \frac{\vec{r}}{r^3}
\;\;\;\;\; =\frac{\mu_0}{4\pi}dq.\frac{\vec{v}\times \vec{r}}{r^3} [\frac{d\vec{l}}{dt}=\vec{v}=আধানের বেগ]
∴\vec{B} =\frac{\mu_0}{4\pi}q.\frac{\vec{v}\times \vec{r}}{r^3}
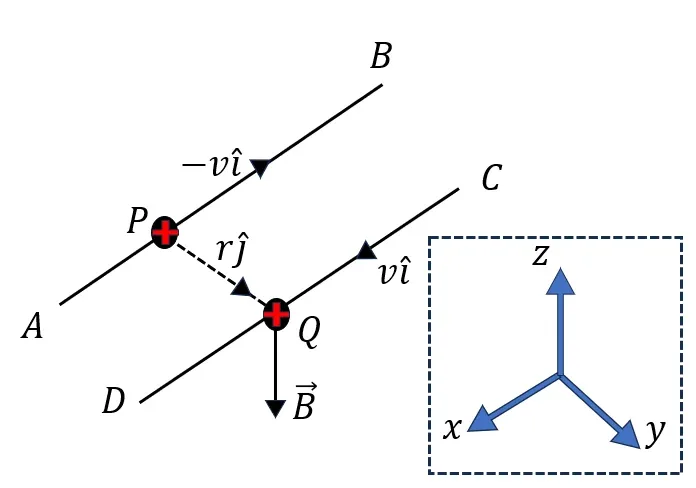
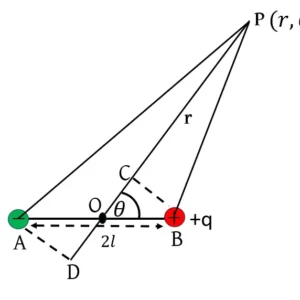
ধরি, AB পথে x অক্ষের সমান্তরালে +q আধান -v\widehat{i} বেগে গতিশীল। এরজন্য, r\widehat{j} লম্ব দূরত্বে Q বিন্দুতে চৌম্বক ক্ষেত্র প্রাবল্য-
\vec{B}=\frac{\mu_0}{4\pi}q.\frac{-v\widehat{i}\times r\widehat{j}}{r^3}
\;\;\;\;\;=-\frac{\mu_0}{4\pi}q.\frac{v.r}{r^3}\widehat{k}
\;\;\;\;\;=-\frac{\mu_0}{4\pi}q.\frac{v}{r^2}\widehat{k}
CD পথে v\widehat{i} ধবমান অপর +q আধানের ওপর Q বিন্দুতে থাকাকালীন অবস্থায় ক্রিয়াশীল চৌম্বক বল,
\vec{F}_m=q(v\widehat{i}\times \vec{B})
\;\;\;\;=-q(v\widehat{i}\times \frac{\mu_0}{4\pi}q.\frac{v}{r^2}\widehat{k})
\;\;\;\;=\frac{\mu_0}{4\pi}\frac{q^2 v^2}{r^2} \widehat{j}
ওই মুহূর্তে, Q বিন্দুতে অবস্থিত +q আধানের ওপর ক্রিয়াশীল কুলম্বীয় তড়িৎ বল,
\vec{F}_e=\frac{1}{4\pi \epsilon_0}\frac{q.q}{r^2}\widehat{j} = \frac{1}{4\pi \epsilon}\frac{q^2}{r^2}\widehat{j}
∴F_m :F_e=\frac{\mu_0}{4\pi}\frac{q^2 v^2}{r^2}:\frac{1}{4\pi \epsilon_0}\frac{q^2}{r^2}
\;\;\;\;=\mu_0 v^2:\frac{1}{\epsilon_0}
\;\;\;\;= v^2:\frac{1}{\mu_0 \epsilon_0}
\;\;\;\;= v^2:c^2 [ \because\;c=\sqrt{\frac{1}{\mu_0 \epsilon_0}} ]
\;\;\;\;= \frac{v^2}{c^2}:1














 ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠