এখানে যে বিষয়গুলি আছে
Toggle1. এক মাত্রিক গতি-সঠিক উত্তরটি বেছে নাও
1.1 একটি বস্তুর ত্বরণ- সময় লেখচিত্রটি দেওয়া আছে। বেগ-সময় লেখচিত্রটি কেমন হবে? 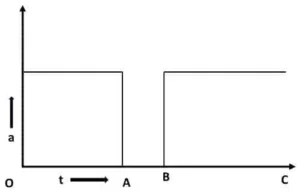
A) 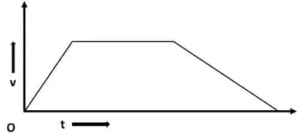 B)
B) 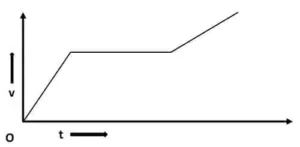 C)
C) 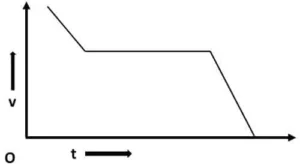 D)
D) 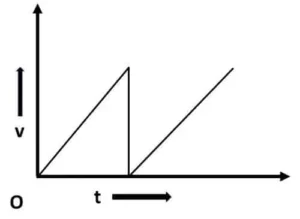
=> OA সময় পর্যন্ত নির্দিষ্ট ত্বরণ আছে। এই সময় কণার বেগ ক্রমশ বৃদ্ধি পাবে।
AB পর্যন্ত ত্বরণ শূণ্য। তাই এইটুকু সময় কণাটী সমবেগে চলবে।
BC পুযন্ত আবার সমত্বরণ থাকায় কণাটির বেগে আবার বৃদ্ধি পেতে থাকবে।
সেজন্য উত্তর হবে option B
1.2 A particle is projected with velocity v_0 along x axis. A damping force is acting on the particle which is proportional to the square of distance from the origin i.e. ma=-{\alpha}x^{2}. The distance at which the particle stops: a) (\frac{2m{{v}_{o}}^{2}}{3\alpha }{)}^{\frac{1}{2}} b)(\frac{3m{{v}_{o}}^{2}}{2\alpha }{)}^{\frac{1}{2}} c) (\frac{3m{{v}_{o}}^{2}}{2\alpha }{)}^{\frac{1}{3}} d) (\frac{2m{{v}_{o}}^{2}}{3\alpha }{)}^{\frac{1}{3}} [JEE,feb-22]
ma=-\alpha {x}^{2}\phantom{\rule{0ex}{0ex}}\\or,\frac{dv}{dt}=-\frac{\alpha }{m}{x}^{2}\phantom{\rule{0ex}{0ex}}\\or,\frac{dv}{dx}\frac{dx}{dt}=-\frac{\alpha }{m}{x}^{2}\phantom{\rule{0ex}{0ex}}\\or,v\frac{dv}{dx}=-\frac{\alpha }{m}{x}^{2}\phantom{\rule{0ex}{0ex}}vdv=-\frac{\alpha }{m}{x}^{2}dx\phantom{\rule{0ex}{0ex}}\\or,\int _{{v}_{0}}^{0}vdv=-\frac{\alpha }{m}\int _{o}^{x}{x}^{2}dx\phantom{\rule{0ex}{0ex}}\\or,{{(\frac{{v}^{2}}{2})}_{{v}_{0}}}^{0}=-\frac{\alpha }{m}{{(\frac{{x}^{3}}{3})}_{{0}_{}}}^{x}\phantom{\rule{0ex}{0ex}}\\or,\frac{{{v}_{0}}^{2}}{2}=-\frac{\alpha }{3m}{x}^{3}\phantom{\rule{0ex}{0ex}}\\so, x=(\frac{{3m}_{}}{2\alpha }{{v}_{0}}^{2}{)}^{\frac{1}{3}}1.3 দ্বিমাত্রিক স্থানে একটি বস্তুর গতির সমীকরণ x = 5t2+2, y = 2t2+5 | বস্তুটির গতিপথ একটি A) অধিবৃত্ত B) সরলরেখা C) বৃত্ত D) পরাবৃত্ত
=> x = 5t2+2 or, t2 = (x-2)/5
এবং y = 2t2+5 or, t2 = (y-5)/2
t2 এর মান তুলনা করে পাই....
(x-2)/5 = (y-5)/2 or, 2x-4 = 5y-25 or, 2x-5y+21 = 0
এটি একটি সরল রেখার সমীকরণ।
1.4 X-অক্ষ বরাবর একটি কণার সরণের সমীকরণ, x = 40 + 12t- t3। থামার আগে কণাটি কতদূর যাবে ?—(A) 16 m, (B) 40 m, (C) 56 m, (D) 36 m
=> x = 40 + 12t - t^3 or, v = \frac{dx}{dt} = 0 + 12 - 3t^2
v = 0 হলে, 12 - 3t^2=0 or, t^2=\frac{12}{13} or,t=2 [t এর ধনাত্মক মান গৃহীত]
t=0 সময়ে, x = 40 + 12.2 - 2^3 = 56
1.5 t = 0 সময়ে x = 0 বিন্দুতে থাকা একটি বস্তু x-অক্ষ বরাবর v = a√x বেগে চলতে শুরু করল। বস্তুটির সরণ ও সময়ের মধ্যে সম্পর্কটি
হল – (A) x ∝ t, (B) x ∝ √t, (C) x∝ t2 (D) কোনোটিই নয়।
=> v = a√x
or, \frac{dx}{dt} = a√x
or, \int x^{ - \frac{1}{2}}dx = \int adt
or, 2x^{\frac{1}{2}} = adt + c
t=0 হলে, x=0. 20^{\frac{1}{2}} = a.0 + c ∴ c=0
or, 2\sqrt{x} = at + c
or, x = \frac{{a}^2}{4}{t}^2 ∴x∝t2
1.6 একটি বল অভিকর্ষের প্রভাবে অবাধে পড়ছে। 0 – 3 sec এবং 4 – 5 sec সময়ের ব্যবধানে বলটির অতিক্রান্ত দূরত্বের অনুপাত হল (A) 1 : 1, (B) 1:16, (C) 9 : 16, (D) 16 : 25
=> প্রাথমিক বেগ u=0
0 – 3 sec সময় পরে x = \frac{1}{2}g3^2 = \frac{9}{2}g
4 – 5 sec সময়ে অর্থাৎ 5th সেকেন্ডে অতিক্রান্ত দূরত্ব x4= \frac{g}{2}(2 \times 5 - 1) = \frac{9}{2}g
দূরত্বের অনুপান x:x4= \frac{9}{2}g:\frac{9}{2}g = 1:1
1.7 t সময়ে একটি বস্তুর অবস্থান ভেক্টর \overrightarrow{r} = 4t^2\widehat{i} + 3t^2\widehat{j} + 2\widehat{k}। বস্তুটির ত্বরণের মান হবে –(A) 5 m·s-2, (B) 10 ms-2, (C) 8 m.s−2, (D) 0
=> বেগ, \overrightarrow{v} = \frac{d\overrightarrow{r}}{dt} = 4\times2t\widehat{i} + 3\times2t\widehat{j} + 0 = \overrightarrow{v} = \frac{d\overrightarrow{r}}{dt} = 8t\widehat{i} + 6t\widehat{j}
ত্বরণ, \overrightarrow{a} = \frac{d\overrightarrow{v}}{dt} = 8\widehat{i} + 6\widehat{j}= a = \sqrt{8^2 + 6^2} = 10
1.8 স্থিরাবস্থা থেকে একটি গাড়ি যাত্রা শুরু করে সমত্বরণে চলছে। n তম সেকেন্ড ও n সেকেন্ডে গাড়িটির দ্বারা অতিক্রান্ত দূরত্বের অনুপাত – (A) \frac{2n - 1}{2n^2} (B) \frac{n^2}{2n - 1} (C) \frac{2n - 1}{n^2} (D) \frac{1}{n^2}
=> {S}_{n} = \frac{1}{2}a(2n - 1) এবং S = \frac{1}{2}an^2
∴S:Sn=\frac{1}{2}a(2n - 1):\frac{1}{2}an^2 = \frac{2n - 1}{n^2}
1.9 একটি বস্তু স্থির অবস্থা থেকে সমত্বরণে যাত্রা শুরু করে প্রথম 10 সেকেন্ডে x দূরত্ব এবং পরবর্তী 20 সেকেন্ডে y দূরত্ব অতিক্রম করে। x এবং y-এর মধ্যে সম্পর্কটি হল – (a) y = x, (b) y = 2x, (c) y = 8x, (d) y = 4x
=> x = প্রথম 10s এ অতিক্রান্ত দূরত্ব = \frac{1}{2}a10^2
y = পরের 20s এ অতিক্রান্ত দূরত্ব = (30s এ অতিক্রান্ত দূরত্ব) - (প্রথম 10s এ অতিক্রান্ত দূরত্ব) = \frac{1}{2}a30^2 - x = 32×\frac{1}{2}a10^2-x = 9x-x = 8x
2. এক মাত্রিক গতি-অতিসংক্ষপ্ত প্রশ্নোত্তর
2.1 গতিশীল কণার গড়বেগ ও তাৎক্ষণিক বেগ কখন সমান হবে?
=> যখন বস্তুটি সমবেগে যাবে।
2.2 বেগ-সময় লেখচিত্রের ক্ষেত্রফল কী প্রকাশ করে।
=> সরণ বোঝায়
2.3 সমদ্রুতিতে বক্র পথে চলমান কোন কণার ত্বরণ থাকতে পারে কি?
=> হ্যাঁ থাকতে পারে। বক্র পথে চললে মান একই থাকলেও অভিমুখের পরিবর্তন হবে। অর্থাৎ ত্বরণ আছে।
2.4 সময়ের সাপেক্ষে ত্বরণের পরিবর্তনের হারের একক লেখো।
=> ত্বরণের পরিবর্তনের হার= \frac{ms^{-2}}{s}=ms^{-3}
2.5 শূন্য ভেক্টর কী? এর তাৎপর্য লেখ।
=> যে ভেক্টরের মান শূন্য তাকে শূন্য ভেক্টর। এর দ্বারা বোঝানো হয় যে দুটি সমান ও বিপরীত মানের ভেক্টর ক্রিয়া করছে। অথবা ক্রিয়ারত একাধিক ভেক্টরের লব্ধি শূন্য।
3 এক মাত্রিক গতি-সংক্ষিপ্ত প্রশ্নোত্তর
স্মার্টফোন বা মোবাইলে দেখার সুবিধার্থে ফোনটি Landscape বা Auto rotate করে নিন।
3.1 দুটি বস্তুকণা একই স্থান থেকে একই দিকে যথাক্রমে 'u' স্থির বেগে এবং 'a' স্থির ত্বরণে চলতে শুরু করল। দেখাও যে, দ্বিতীয় কণাটি যে মুহূর্তে প্রথম কণাটিকে অতিক্রম করে তখন তার বেগ হয় 2u
=> প্রথম কণার সমবেগ = u
দ্বিতীয় কণার প্রাথমিক বেগ = 0
ধরি, t সময় পরে কণা দুটি মিলিত হবে। অবশ্যই কণা দুটি একই স্থান থেকে যাত্রা শুরু করা থেকে মিলিত হওয়া পর্যন্ত সমান দূরত্ব অতিক্রম করবে।
ধরি এই দূরত্ব s। তাহলে প্রথম কণার ক্ষেতে s= ut এবং দ্বিতীয় কণার ক্ষেত্রে s= \frac{1}{2}at2
অর্থাৎ ut = \frac{1}{2}at2 or, 2u = at .....(i)
দ্বিতীয় কণার অন্তিম বেগ হবে, v = o + at = 2u [(i) নং সমীঃ থেকে] (প্রমাণিত)



 ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠