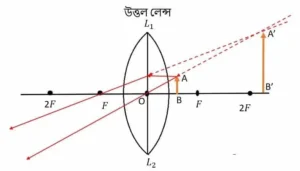
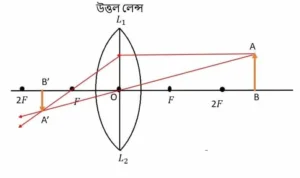
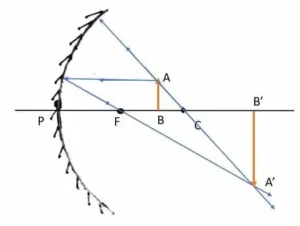
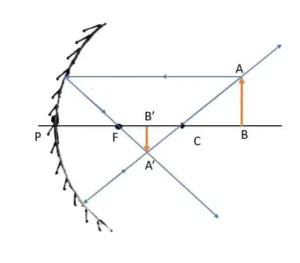
এখানে যে বিষয়গুলি আছে
Toggle1. নিউটনের গতিসূত্র-সঠিক উত্তরটি বেছে নাও
স্মার্টফোন বা মোবাইলে দেখার সুবিধার্থে ফোনটি Landscape বা Auto rotate করে নিন।
1.1 4 kg, 2 kg ও 1 kg ভরের তিনটি ব্লককে একটি ঘর্ষণহীন তলের ওপর পরস্পরের সংস্পর্শে রাখা আছে। 14 N মানের একটি বল 4 kg ব্লকের ওপর
প্রযুক্ত হল | তাহলে 4 kg ও 2 kg ব্লক দুটির মধ্যে পারস্পরিক সংস্পর্শ বল হবে- A) 4N B) 6N C) 8N D) 10N
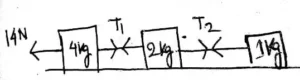 ত্বরণ= \frac{14}{4 + 2 + 1}m/ s^2=2m/s2। T1 =(2+1)kg.2m/s2 =6N
ত্বরণ= \frac{14}{4 + 2 + 1}m/ s^2=2m/s2। T1 =(2+1)kg.2m/s2 =6N
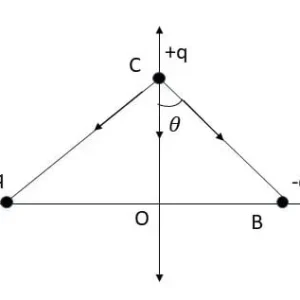
1.2 চিত্রে কপিকল এবং সুতোগুলো মসৃণ এবং এদের ভর উপেক্ষণীয়। এই সংস্থাটি সাম্যাবস্থায় থাকলে θ এর মান কত হবে। A) 00 B) 300 C) 450 D) 600
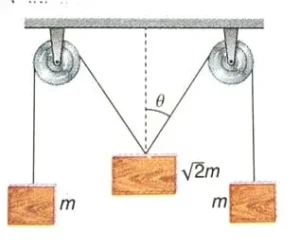 => প্রতিটি সুতোয় সমান টান হবে। এর মান T হলে; m ভরের বস্তুগুলির জন্য T=mg
=> প্রতিটি সুতোয় সমান টান হবে। এর মান T হলে; m ভরের বস্তুগুলির জন্য T=mg
√2m ভরের দুটি সুতোদুটির জন্য;
Tcosθ+Tcosθ = √2mg
or, 2Tcosθ = √2mg
or, Tcosθ = \frac{1}{\sqrt{2}}mg
or, mgcosθ = \frac{1}{\sqrt{2}}mg
or, cosθ= \frac{1}{\sqrt{2}}
∴ θ = 450
1.3 একটি বন্দুক থেকে বুলেট ছোড়া হল। বুলেটের ওপর ক্রিয়াশীল বলটি হল F = 600 - 2 × 105t, যেখানে F নিউটন এককে এবং t সেকেন্ড এককে
প্রকাশিত |বন্দুক থেকে নির্গত হওয়ার পরমুহূর্তে বুলেটের ওপর ক্রিয়াশীল বল শূন্য। বুলেটের ওপর প্রযুক্ত গড় বলের ঘাত- A) 1.8 N.s B) শূন্য C) 9N.s D) 0.9 N.s
=> F = 600 - 2 × 105t । বন্দুক থেকে বুলেট নির্গত হবার পর বল= 0 অর্থাৎ 600 - 2 × 105t = 0 or, t = \frac{600}{2 \times {10}^5}s = 3×10-3s
বলের ঘাত, I= \int Fdt
=\underset{0}{\overset{3 \times {10}^{ - 3}}{\int }}(600 - 2 \times {10}^5t)dt
= {{(600t - 2 \times {10}^5 \times \frac{t^2}{2})}_{0}}^{3 \times {10}^{ - 3}}
=[600 \times 3 \times {10}^{ - 3} - {10}^5 \times (3 \times {10}^{ - 3})^2] - [0 - 0]
=1.8-0.9
=0.9
1.4 w ওজনের এক ব্যক্তি a ত্বরণসহ ঊর্ধবগামী একটি লিফটের ওপর দাঁড়িয়ে আছে। যদি অভিকর্ষজ ত্বরণ g হয় তবে লোকটির আপাত ওজন হবে- (A) w(1 + \frac{a}{g}) (B) w(1 -\frac{a}{g}) (C) w (D) শূন্য
=> প্রতিক্রিয়া বল R। ব্যক্তির ভর m =\frac{w}{g}
বলের সমীকরণ-
ma=R-mg
or, R= ma+mg = mg(\frac{a}{g}+1)= w(1+\frac{a}{g})
এটিই আপাত ওজন।
1.5 m ভরের একটি মুক্ত বস্তুকণা ভূমি থেকে স্থির উচ্চতায় একটি অনুভূমিক তলে (xy- তল) x অক্ষ বরাবর গতিশীল ছিল। হঠাৎ বিস্ফোরণের ফলে কণাটি ভেঙ্গে \frac{m}{4} এবং \frac{3m}{4} ভরের দুটি কণা তৈরি হল। এক মুহূর্ত পরে y অক্ষ বরাবর ছোটো কণাটির অবস্থান হল y= +15 cm। ওই মুহূর্তে বড়ো কণাটির অবস্থান হল- (A) -5 cm (B) +20 cm (C) +5 cm (D) -20 cm
=> ভরবেগের সংরক্ষণ নীতি অনুযায়ী,
m_1 v_1+m_2 v_2=0
or, m_1 v_1=-m_2 v_2
or, m_1 \frac{y_1}{\cancel{t}}=-m_2 \frac{y_2}{\cancel{t}}
or, \frac{m}{4}.15=-\frac{3m}{4}.y_2
\therefore y_2 = -5 cm
1.6 40 kg ভরসম্পন্ন একটি বাঁদর একটি দড়ি বেয়ে ওপরে ওঠার চেস্টা করছে। দড়িটি সর্বাধিক 600 N টান সহ্য করতে পারে। নিম্নলিখিত কোন্ ক্ষেত্রে দড়িটি ছিঁড়ে যাবে?
(A) বাঁদরটি যখন 6 m.s-2 ত্বরণসহ ওপরে উঠতে শুরু করে।
(B) বাঁদরটি যখন 4 m.s-2 ত্বরণসহ ওপরে নীচে নামতে শুরু করে।
(C) বাঁদরটি যখন 5 m.s-1 সুষম বেগে ওপরে উঠতে শুরু করে। 
=> বাঁদরের ওজন 40×10 N= 400 N
সর্বাধিক টান 600 N হলে দড়িতে বাঁদর দ্বারা সর্বাধিক বল প্রয়োগ (600-400) N = 200 N
সর্বাধিক ত্বরণ \frac{200}{40}m.s-2 = 5 m.s-2
অর্থাৎ বাঁদরটি যখন 5 m.s-2 ত্বরণের বেশি বেগে ওপরে উঠতে শুরু করবে তখনই দড়্রি ছিঁড়ে যাবে। সুতরাং উত্তর হবে (A)
1.7 মসৃণ অনুভূমিক তলে স্থির অবস্থায় রাখা একটি পাটাতনের ওপর দিয়ে একটি লোক পাটাতনের সাপেক্ষে v বেগে বাঁদিক থেকে ডানদিকে ছুটে গেলে পাটাতনের পাটাতনের বেগ কত হবে? (লোকটি ও পাটাতনের ভর যথাক্রমে m ও M)
(A) \frac{Mv}{M+m} বাঁদিকে (B) \frac{Mv}{M+m} ডানদিকে (C) \frac{mv}{M+m} বাঁদিকে (D) \frac{mv}{M+m} ডানদিকে
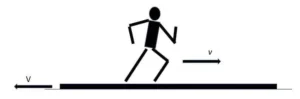
=>পাটাতনের বেগ V।
ভূমির সাপেক্ষে ব্যক্তির বেগ V-(-v)=V+v
ভরবেগের সংরক্ষণ নীতি অনুযায়ী
m(V+v) + MV = 0
or, mV+mv+MV=0
or, (m+M)V=-mv
∴V=-\frac{mv}{M+m}
v ডানদিকে হলে V বাঁদিকে হবে।
1.8 সরলরেখায় একটি নির্দিষ্ট গতিবেগে চলমান 4 kg ভরের একটি গোলক A আর-একটি স্থির 1 kg ভরের গোলক B কে ধাক্কা মারে। সংঘর্ষের পরে A এবং B যথাক্রমে v_1 m/s এবং v_2 m/s বেগে A এর প্রাথমিক গতিবেগের অভিমুখের সঙ্গে যথাক্রমে 300 ও 600 কোণে চলতে থাকে। \frac{v_1}{v_2} এর মান হবে-
(A) \frac{\sqrt{3}}{4} (b) \frac{4}{\sqrt{3}} (C) \frac{1}{\sqrt{3}} (D) \sqrt{3}
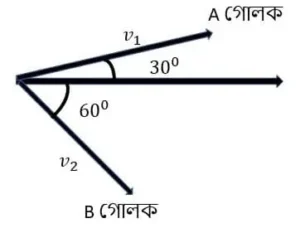
সংঘর্ষের আগে গোলকদুটির Y অক্ষ বরাবর কোনো ভরবেগের উপাংশ নেই। তাহলে সংঘর্ষের পরেও থাকবে না।
অর্থাৎ, m_1 v_1sin300=m_2 v_2sin60
or, 4×v_1 \times\frac{1}{2} = 1×v_2×\frac{\sqrt{3}}{2}
∴ \frac{v_1}{v_2}=\frac{\sqrt{3}}{4}
2. নিউটনের গতিসূত্র-অতি সংক্ষিপ্ত প্রশ্নোত্তর
3. নিউটনের গতিসূত্র-সংক্ষিপ্ত প্রশ্নোত্তর
স্মার্টফোন বা মোবাইলে দেখার সুবিধার্থে ফোনটি Landscape বা Auto rotate করে নিন।
3.1 একটি দমকলের জেট থেকে 12.2 m/s বেগে একটি দেয়ালের ওপর লম্বভাবে জল ফেলা হচ্ছে। দেয়ালের ওপর প্রযুক্ত চাপ নির্ণয় করো ।
=> ধরি, দেওয়ালের A m2 ক্ষেত্রফলে লম্বভাবে জল পড়ছে।
জলের বেগ 12.2 m/s হলে জল প্রবাহের হার= \frac{আয়তন}{সময়} = \frac{দৈর্ঘ্য \times প্রস্থচ্ছেদ}{সময়} = \scriptsize{বেগ \times প্রস্থচ্ছেদ} = 12.2×A m3/s
একক সময়ে আপতিত জলের ভর = \frac{আয়তন}{সময়}×জলের ঘনত্ব
or, \frac{জলের\,ভর}{সময়}= 12.2A×103 kg/s [জলের ঘনত্ব 103 kg/m3]
দেওয়ালে জল আঘাতের পর জলের বেগ শূণ্য হয়ে যায়।
তাহলে ঘাত = বল×সময় = ভরবেগের পরবর্তন
or, বল = \frac{জলের\,ভর}{সময়}\times \scriptsize{ভরবেগের\,পরিবর্তন} = 12.2A×103(12.2-0) N = 1.49×105A N (প্রায়)
∴ চাপ= \frac{বল}{ক্ষেত্রফল}= \frac{1.49\times10^5 A}{A} Pa = 1.49×105 N
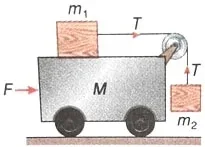 3.2 M ভরের একটি গাড়ির একপ্রান্তে একটি মসৃণ হালকা কপিকল আছে। কপিকলটির ওপর দিয়ে অতিক্রান্ত একটি ভারহীন সুতোর একপ্রান্ত গাড়িটির ওপর রাখা m_1 ভরের একটি ব্লকের সঙ্গে যুক্ত। ওই সুতোটির অপর প্রান্তে m_2 ভরের আরও একটি ব্লক যুক্ত করে ঝুলিয়ে দেওয়া হয়েছে। গাড়িটিতে কত অনুভূমিক বল F প্রয়োগ করলে m_1 ও m_2 ব্লক দুটি গাড়ি সাপেক্ষে স্থির থাকবে?
3.2 M ভরের একটি গাড়ির একপ্রান্তে একটি মসৃণ হালকা কপিকল আছে। কপিকলটির ওপর দিয়ে অতিক্রান্ত একটি ভারহীন সুতোর একপ্রান্ত গাড়িটির ওপর রাখা m_1 ভরের একটি ব্লকের সঙ্গে যুক্ত। ওই সুতোটির অপর প্রান্তে m_2 ভরের আরও একটি ব্লক যুক্ত করে ঝুলিয়ে দেওয়া হয়েছে। গাড়িটিতে কত অনুভূমিক বল F প্রয়োগ করলে m_1 ও m_2 ব্লক দুটি গাড়ি সাপেক্ষে স্থির থাকবে?
=> F বল প্রয়োগে সমগ্র সংস্থাটির ত্বরণ হবে = \frac{F}{m_1+m_2+M}·······(i)
m_1 ভরের বস্তুর ওপর টান T=m_2g
m_1 ভরের বস্তুর ত্বরণ = \frac{m_2g}{m_1}········(ii)
m_1 ও m_2 স্থির থাকবে যখন (i) ও (ii) নং সমীকরণ সমান ও বিপরীত হবে।
সুতরাং, \frac{F}{m_1+m_2+M}= \frac{m_2g}{m_1}
∴ F = \frac{m_2\left(m_1+m_2+M\right)g}{m_1}
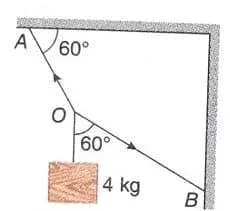
3.3 পাশের চিত্রানুযায়ী 4 kg ভরের একটি ব্লক ঝুলন্ত অবস্থায় রয়েছে। OA এবং OB সুতো দুটিতে টান নির্ণয় করো। (ধরে নাও, g = 10 m/s2)
=>OA ও OB সুতায় টান যথাক্রমে T1 ও T2
অনুভূমিক বরাবর বলের সমীকরণ,
T1 sin30° = T2 sin60°
or, \small{T_1 \frac{1}{2}= T_2\frac{\sqrt3}{2}}
or, \small{T_1 = \sqrt{3}T_2} ······(i)
উল্লম্ব বরাবর বলের সমীকরণ,
T1cos30° = 4×10 + T2cos60° 
or, \small{T_1\frac{\sqrt3}{2} = 40 + T_2\frac{1}{2}}
or, \small{\sqrt{3}T_1 = 80 + T_2}
or, \small{\sqrt3\times\sqrt3T_2 = 80 + T_2}
or, 3T2 — T2 = 80
or, 2T2 = 80
or, T2 = 40 N
(i) নং সমীকরণে T2 এর মান বসাই,
T1 = \small{\sqrt{3}\times 40}=40\sqrt3 N
3.4 L দৈর্ঘ্যের একটি সুতোর সাহায্যে একটি ভারী গোলাকার বস্তু দুলছে। এর দোলনের বিস্তার \theta হলে সুতোয় সর্বোচ্চ টান কত? ধরো, বস্তুটির ওজন w এবং বিস্তার ক্ষুদ্র]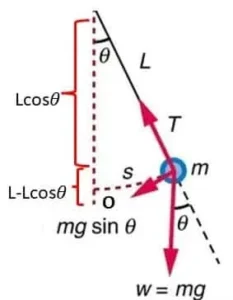
=> টান সর্বোচ্চ হবে সর্বনিম্ন বিন্দুতে (O)
এখন mg=w, বেগ= v হলে টান হবে T=mg + \frac{mv^2}{L}
আবার, সর্বোচ্চ ও সর্বনিম্ন বিন্দুতে শক্তির সংরক্ষণ নীতি অনুযায়ী,
\frac{1}{2}mv^2 = mgL - mgLcos\theta
or, v^2=2gL(1-cos\theta)
or, \frac{v^2}{L}=2g.2sin^{2}\frac{\theta}{2}
or, \frac{v^2}{L}=4g.(\frac{\theta}{2})^{2} [\because \theta ক্ষুদ্র]
\frac{v^2}{L}=g{\theta}^{2}
তাহলে সর্বোচ্চ টান হবে, T=mg + mg{\theta}^{2}=mg(1+{\theta}^{2})=w(1+{\theta}^{2})



 ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠