1. ঘর্ষণ বল -সঠিক উত্তরটি বেছে নাও
1.1 একটি বস্তু θ নতিকোণবিশিষ্ট একটি নততল বরাবর নেমে আসছে। নামার সময় ঘর্ষণ গুণাঙ্ক μ দূরত্বের সঙ্গে সমানুপাতিক (μ=kx) বস্তুটি নততল বরাবর নেমে আসবে
(A) স্থির ত্বরণ gsinθ সহ
(B) স্থির ত্বরণ (gsinθ-μgcosθ) সহ
(C) স্থির ত্বরণ (μgcosθ-gsinθ) সহ
(D) পরিবর্তনশীল ত্বরণসহ
=> ঘর্ষণ গুণাঙ্ক যেহেতু দূরত্বের সাথে সমানুপাতী তাই ত্বরণ পরিবর্তন হতে থাকবে।
1.2 একটি m ভরের ব্লক টেবিলের ওপর স্থিরাবস্থায় রাখা আছে। ব্লক ও টেবিলের মধ্যে ঘর্ষণ গুণাঙ্ক μ । ব্লকটিতে সর্বনিম্ন যে বলের জন্য গতিশীল হবে তা হল-
(A) μmg
(B) \frac{\mu mg}{\sqrt{1+\mu^2}}
(C) mg
(D) কোনোটিই নয়
∴ F_{min}=\frac{\mu mg}{\sqrt{1+\mu^2}}
=>
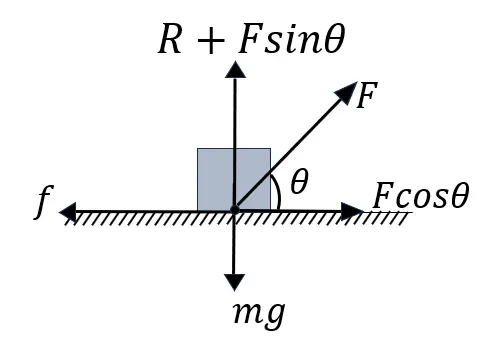স্থির বেগে থাকা অবস্থায় R+Fsin\theta=mg or, R=mg-Fsin\theta এবং
Fcos\theta=f
or, Fcos\theta=\mu R
or, Fcos\theta=\mu (mg-Fsin\theta)
or, Fcos\theta+\mu Fsin\theta=\mu mg
or, F(cos\theta+\mu sin\theta)=\mu mg
or, F=\frac{\mu mg}{cos\theta+\mu sin\theta}
or, F=\frac{\mu mg}{cos\theta+tan\lambda sin\theta} [\lambda=ঘর্ষণ কোণ এবং tan\lambda = \mu]
or, F=\frac{\mu mgcos\lambda}{cos\theta cos\lambda +sin\lambda sin\theta}
or, F=\frac{\mu mgcos\lambda}{cos(\theta-\lambda)}
F সর্বনিম্ন হবে যদি cos(\theta-\lambda)=1 হয়।
এখন, tan\lambda = \mu
or, tan^2\lambda = \mu^2
or, sec^2\lambda-1 = \mu^2
or, sec^2\lambda = 1+\mu^2
or, sec\lambda =\sqrt{ 1+\mu^2}
or, cos\lambda = \frac{1}{\sqrt{ 1+\mu^2}}
উত্তর -(B) \frac{\mu mg}{\sqrt{1+\mu^2}}
1.3 2 kg ভরের একটি ব্লক একটি অনুভূমিক টেবিলের ওপর স্থিরাবস্থায় আছে। ব্লক ও টেবিলের মধ্যে ঘর্ষণ গুণাঙ্ক 0.5। অনভূমিকের সঙ্গে সমান্তরালে 7 N বল ব্লকের ওপর প্রয়োগ করা হলে (ধরো, = 10 m s^{-2} ) –
(A) বস্তুটির ত্বরণ হবে 3 m s^{-2}
(B) ঘর্ষণ বল হবে 10 N
(C) ঘর্ষণ বল হবে 7 N
(D) কোনোটিই নয়।
=> স্থিতি ঘর্ষণ বল, F_s= \mu R = \mu mg= 0.5.2.10 N = 10 N
তারমানে প্রযুক্ত বল 10 N বা তার বেশি হলেই বস্তুটি চলতে শুরু করবে।
এখন প্রযুক্ত বল 7 N হওয়ায় বস্তুটি স্থির অবস্থাতেই থাকবে।
সুতরাং Ans- (C) ঘর্ষণ বল হবে 7 N
1.4 নততল বরাবর স্থির বেগে একটি বস্তু পিছলে নামছে। যদি নততলটির নতিকোণ θ হয়, তাহলে গতীয় ঘর্ষণ গুণাঙ্ক হবে –
(A) sinθ
(B) cosθ
(C) tanθ
(D) কোনোটিই নয়।
=> বস্তুটি স্থির বেগে নামছে। অর্থাৎ সাম্যাবস্থায় আছে। তাহলে μ=tanθ (C )
1.5 একটি পতঙ্গ একটি অর্ধগোলকের তল বরাবর খুব ধীরে 1 cm উচ্চতায় উঠতে পারে। অর্ধগোলকটির ব্যাসার্ধ 5 cm এবং পতা অর্ধগোলকের ঘর্ষণ গুণাঙ্ক μ হলে —
(A) \mu \geq \frac{3}{4}
(B) \mu \geq \frac{3}{5}
(C) \mu \geq \frac{4}{5}
(D) কোনোটিই নয়
=>
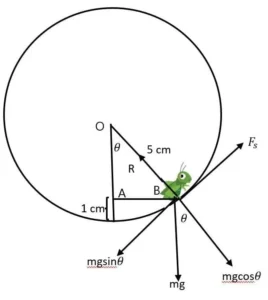F_s=\mu\ R
or, mgsin\theta=\mu\ mgcos\theta
or, tan\theta=\mu
আবার, AB=\sqrt{{OB}^2-{OA}^2}= \sqrt{5^2-4^2}= 3
\therefore\mu=tan\theta=\frac{AB}{OA}=\frac{3}{4}
1.6 একটি ঘাত বল 2 kg ভরের ব্লকে 10 m/s গতিবেগ তৈরি করে। ব্লকটি যে অনুভূমিক তলে রয়েছে তার ঘর্ষণ গুণাঙ্ক 0.2। ব্লকটি কত দূরত্ব অতিক্রম করবে?
(A) 20 m
(B) 25 m
(C ) 50 m
(D) কোনোটিই নয়
=> u= 10 m/s, F_s= \mu R= \mu mg=0.2×2×10 N=4 N
a_s=\frac{F_s}{m}=\frac{4}{2}=2 m/s2
s=\frac{u^2}{2a_s}=\frac{10^2}{2\times 2}m =25 m
1.7 অনুভূমিকভাবে 5 N বল প্রয়োগ করে 0.1 kg ভরের একটি ব্লককে উল্লম্ব দেয়ালের গায়ে চেপে রাখা হয়েছে। ব্লক ও দেয়ালের মধ্যে ঘর্ষণ গুণাঙ্ক 0.5 হলে ব্লকের উপর ক্রিয়াশীল ঘর্ষণ বলের মান হল-
(A) 2.5 N
(B) 0.98 N
(C) 4.9 N
(D) 0.49 N
=>এক্ষেত্রে ঘর্ষণ বল দেওয়ালের সমান্তরালে লম্বভাবে উপরের দিকে ক্রিয়া করবে।
প্রতিক্রিয়া বল, R = 5 N। ব্লকটি যেহেতু আটকে আছে তাই স্থিত ঘর্ষণ বল, F_s=\mu R = 0.5\times 5 N = 2.5 N
1.8 m ভর ও p ভরবেগসম্পন্ন একটি বস্তু একটি অমসৃণ অনুভূমিক তলের ওপর দিয়ে চলছে। বস্তুটিকে x দূরত্বে থামানো হলে বস্তু ও তলের মধ্যে ঘর্ষণ গুণাঙ্ক হবে -
(A) \mu = \frac{p^2}{2gm^2x}
(B) mu = \frac{p^2}{2gmx}
(C) \mu = \frac{p}{2gmx}
(D) \mu = \frac{p}{2gm^2x}
=> F_k=\mu_k R আবার, F_k=ma_k
∴ \mu_k R =ma_k
or, \mu_k=\frac{ma_k}{R}=\frac{ma_k}{mg}
or, \mu_k=\frac{a_k}{g}
এখন, প্রাথমিক বেগ, u=\frac{p}{m}, অন্তিম বেগ=0।
∴ 0^2=u^2-2a_k x
or, 2a_k x=u^2
or, a_k=\frac{u^2}{2x}=\frac{p^2}{2m^2 x}
∴ \mu_k=\frac{p^2}{2m^2gx}
1.9 অনুভূমিক তলের ওপর স্থির অবস্থায় রাখা একটি 5 kg ওজনের কাঠের ব্লকের মধ্যে একটি 50 g ওজনের গুলি ছোঁড়া হল। ব্লক ও তলের মধ্যে চল ঘর্ষণ গুণাঙ্ক হল 0.2। গুলিটি ছোঁড়ার পর ব্লকটির মধ্যে গুলিটি প্রবেশ করায় ব্লকটি 5 m দূরে সরে গেল। তাহলে গুলিটির বেগ হল-
(A) 101 m/s
(B) 202 m/s
(C) 303 m/s
(D) 447 m/s
=> গুলিসহ ব্লকের ভর (m)=(5+0.050) kg=5.05 kg
ma_k=F_k=\mu_kR=\mu_kg
or, a_k=\mu_kg
\;\;\;\;\;=0.2×9.8 m/s^2=1.96m/s^2
সরণ(s)=5 m, সংঘর্ষের পরে গুলিসহ ব্লকের বেগ u।
∴ 0^2=u^2-2a_ks
or, u^2=2×1.96×5=19.6
or, u=4.43 m/s
ধরি, গুলির প্রাথমিক বেগ u_1।
ভরবেগের সংরক্ষণ সূত্র-
গুলির ভরবেগ=ব্লকসহ গুলির ভরবেগ
or, 0.05×u_1=5.05×4.43
or, u_1=\frac{5.05×4.43}{0.05}=447.43 m/s
1.10 30 kg ভরের একটি বস্তু অনুভূমিক অমসৃণ তলের ওপর রাখা আছে। বস্তুটির ওপর 200 N বল প্রয়োগ করলে বস্তুটি 2s সময়ে স্থির অবস্থা থেকে 4 m/s দ্রুতি লাভ করে। ঘর্ষণ গুণাঙ্কের মান হবে -
(A) 0.476 (প্রায়)
(B) 0.45
(C) 0.43
(D) 0.40 |
=> F=220N, m=30 kg
মোট ত্বরণ (a_k)=\frac{4-0}{2}=2 m/s^2
ma_k=F-F_s=F-\mu mg
or, 30×2=200-\mu×30×9.8
or, 294\mu=200-60
or, \mu=\frac{140}{294}=0.476
1.11 2 kg ভরের কোনো ব্লক অনুভূমিক রাস্তায় রাখা আছে। ব্লক ও রাস্তার মধ্যে ঘর্ষণ গুণাঙ্ক 0.2। যদি ব্লকের ওপর 6 N অনুভূমিক বল প্রয়োগ করা হয়, তবে প্রথম সেকেন্ডে অতিক্রান্ত দূরত্ব হবে -
(A) 1 m,
(B) 0.9 m
(C)0.5 m
(D) 0.8 m ।
=> ma_k=F-\mu mg
or, a_k=\frac{F-\mu mg}{m}
or, \;\;\;\;=\frac{6-0.2×2×9.8}{2}m/s^2
or, \;\;\;\;=1.04 m/s^2
1 সেকেন্ডে অনিক্রান্ত দূরত্ব s=\frac{1}{2}a_k t^2
\;\;\;\;\;\;=\frac{1}{2}×1.04× 1^2 m
\;\;\;\;\;\;=0.52 m
3.2 L দৈর্ঘ্যের একটি চেন টেবিলের ওপর রাখা আছে। তার দৈর্ঘ্যের l অংশ টেবিলের বাইরে ঝুলছে। টেবিল ও চেনের মধ্যে ঘর্ষণ গুণাঙ্ক μ হলে, l -এর সর্বোচ্চ মান কত হবে? Ans: \frac{\mu L}{1+\mu}
=>
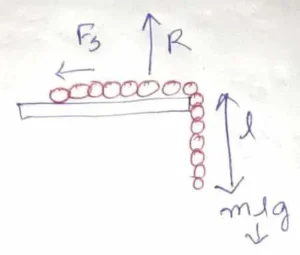চেনের একক দৈর্ঘ্যের ভর m।
ঝুলন্ত l অংশের ওজন mlg=F
অবশিষ্ট (L-l) অংশের ওজন (L-l)mg=R
সাম্যাবস্থায়,
F_s = \mu R
কিন্তু, F_s = F
or, \mu R=mlg
or, \mu m(L-l)g=mlg
or, \mu L-\mu l=l
or, \mu L=l+\mu l
or, l(1+\mu )= \mu L
or, l=\frac{\mu L}{1+\mu}
3.3 একটি বস্তু । বস্তুটিকে ওই তল বরাবর উপরের দিকে u বেগে প্রক্ষেপ করলে দেখাও যে, বস্তুটি নততল বরাবর \frac{u^2}{4gsin\theta} দূরত্ব পর্যন্ত উঠবে।
=>
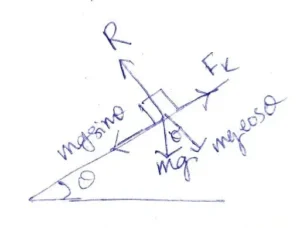
ধরি ভর m, ঘর্ষণ বল f, প্রতিক্রিয়া বল R, ঘর্ষণ গুণাঙ্ক \mu ।
সমবেগে নামলে, mgsin\theta= f
or, mg sin\theta= \mu R
or, mgsin\theta= \mu mgcos\theta
or, tan\theta = \mu
ওপরে ওঠার সময় প্রযুক্ত বল
or, ma=mgsin\theta+f
or, ma=mgsin\theta+\mu R
or, ma=mgsin\theta+\mu mg cos\theta
or, a=g(sin\theta+\mu cos\theta)
u বেগে তল বরাবর নিক্ষেপ করলে যদি s দূরত্ব যায় তাহলে,
u^2-2as=0
or, s = \frac{u^2}{2a} = \frac{u^2}{2g(sin\theta+\mu cos\theta)} =\frac{u^2}{2g(sin\theta+tan\theta cos\theta)}=\frac{u^2}{2g(sin\theta+sin\theta)}=\frac{u^2}{4gsin\theta}
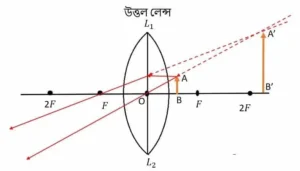
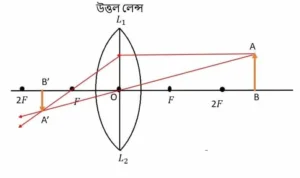
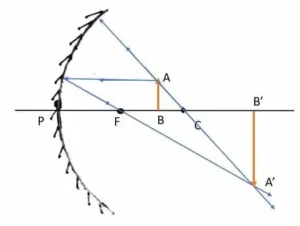
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠
