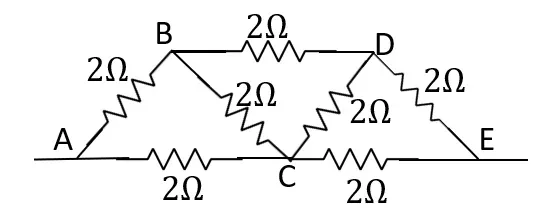
প্রদত্ত বর্তনির তুল্য রোধ নির্ণয় কর।
উত্তর-
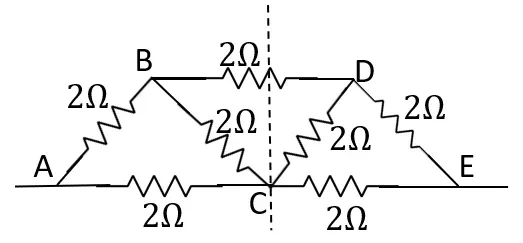
দাগের দুই পাশের অংশ বস্তু প্রতিবিম্বের ন্যায়। তাই BC ও CD একই প্রবাহ যাবে। অর্থাৎ AE এর সঙ্গে C যুক্ত না করলেও হবে।
তাহলে বর্তনি হবে নিম্নরূপ-
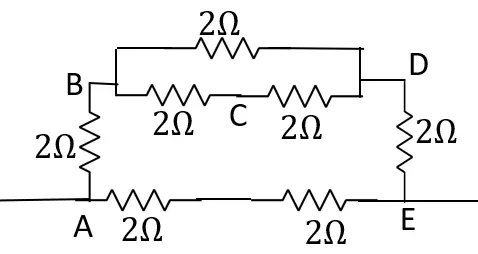
BD অংশে তুল্য রোধ R_1 হলে,
R_1=(2||(2+2))\Omega
\;\;\;=(2||4)\Omega
\;\;\;=(\frac{1}{2}+\frac{1}{4})^{-1}\Omega
\;\;\;=(\frac{2+1}{4})^{-1}\Omega
\;\;\;=\frac{4}{3}\Omega
AB, R1 ও DE শ্রেণি সমবায়ে থাকায় এদের তুল্য রোধ,
R_2=(2+\frac{4}{3}+2)\Omega = (4+\frac{4}{3})\Omega
=(\frac{12+4}{3})\Omega =(\frac{16}{3})\Omega
AE শাখা ও R2 সমান্তরাল সমান্তরাল সমবায়ে আছে।
∴ বর্তনির তুল্য রোধ, (\frac{16}{3}||(2+2))\Omega =(\frac{16}{3}||4)\Omega
(\frac{3}{16}+\frac{1}{4})^{-1}\Omega=(\frac{3+4}{16})^{-1}\Omega=\frac{16}{7}\Omega
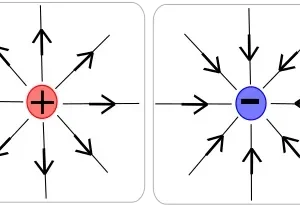
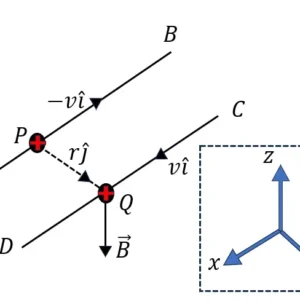
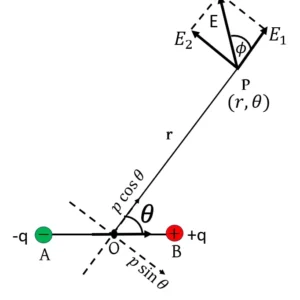
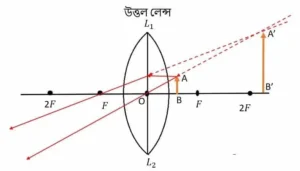
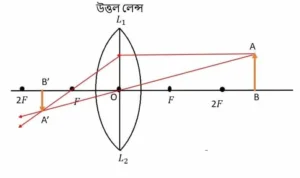
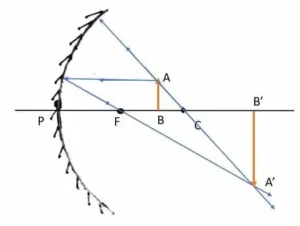
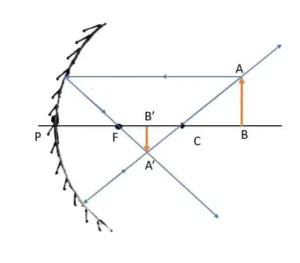
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠