পদার্থ বিজ্ঞানের সূত্রসমূহ

এখানে যে বিষয়গুলি আছে

সূত্র- একমাত্রিক গতি (One-Dimensional Motion)

1. গড় বেগ: V_a= $\frac{মোট সরণ}{মোট সময়}$
2. অন্তিম বেগ: v=u+at [u=প্রাথমিক বেগ, a= ত্বরণ, t=সময়]
3. সরণ: s= $ut+\frac{1}{2}at^2$
4. $v^2=u^2+2as$
5. t-তম সময়ে সরণ: $s_t=u+\frac{1}{2}a(2t-1)$

সূত্র- ভেক্টর (Vector)

ভেক্টরের যোগ

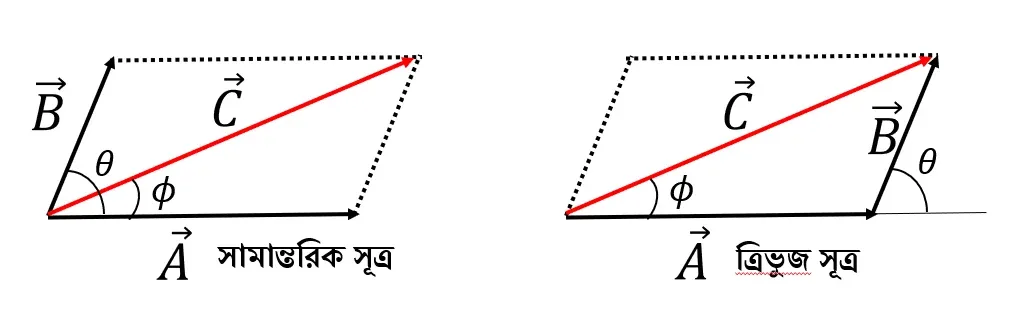
$\overrightarrow{A} + \overrightarrow{B} = \overrightarrow{C}$
লব্ধি ভেক্টরের মান, $C = \sqrt{A^2 + B^2 + 2ABcos\theta }$
লব্ধি ভেক্টরের অভিমুখ, $tan \phi = \frac{Bsin\theta}{A + Bcos\theta}$

ভেক্টরের লম্ব উপাংশে বিভাজন

$P=Rcos\theta$ , $Q=Rsin\theta$

ভেক্টরের বিয়োগ

$\overrightarrow{C}=\overrightarrow{A} -\overrightarrow{B} = \overrightarrow{A} +(-\overrightarrow{B})$
লব্ধি ভেক্টরের মান, $C = \sqrt{A^2 + B^2 + 2ABcos(\pi-\theta)}$ = $\sqrt{A^2 + B^2 -2ABcos\theta}$
লব্ধি ভেক্টরের অভিমুখ, $tan \phi = \frac{Bsin\theta}{A - Bcos\theta}$

ভেক্টরের ডট (.) গুণ

ভেক্টরের ক্রস (×) গুণ

$\overrightarrow{A} = A_1\widehat{i} + A_2\widehat{j} + A_3\widehat{k}$ , $\overrightarrow{B} = B_1\widehat{i} + B_2\widehat{j} + B_3\widehat{k}$ ,
$\overrightarrow{A}\times \overrightarrow{B}$ = $\left|\begin{array}{cc} \widehat{i} & \widehat{j} & \widehat{k} \\ A_1 & A_2 & A_3 \\ B_1 & B_2 & B_3 \\ \end{array}\right|$
= $(A_2B_3 - A_3B_2)\widehat{i} - (A_1B_3 - A_3B_1)\widehat{j} + (A_1B_2 - A_2B_1)\widehat{k}$