Table of Contents
Toggleভরকেন্দ্রগামী লম্ব অক্ষের সাপেক্ষে জড়তা ভ্রামক
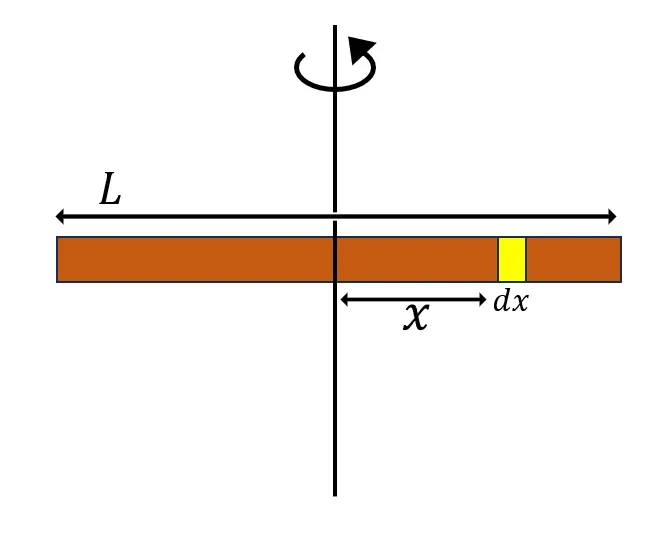
দন্ডের ভর M, দৈর্ঘ্য L। একক দৈর্ঘ্যের ভর m=\frac{M}{L}
দন্ডের মধ্যবিন্দু থেকে x দূরত্বে ক্ষুদ্র দৈর্ঘ্য dx এর ভর mdx।
ভরকেন্দ্রগামী লম্ব অক্ষের সাপেক্ষে জড়তা ভ্রামক I=\sum_{i=1}^{n}{m_ir_i^2}
= \int_{-\frac{L}{2}}^{\frac{L}{2}}{mdxx^2}
=\int_{-\frac{L}{2}}^{\frac{L}{2}}{\frac{M}{L}x^2dx}
=\frac{M}{L}\int_{-\frac{L}{2}}^{\frac{L}{2}}{x^2dx}
=\frac{M}{L}(\frac{x^3}{3})_{-\frac{L}{2}}^{\frac{L}{2}}
=\frac{M}{3L}(x^3)_{-\frac{L}{2}}^{\frac{L}{2}}
=\frac{M}{3L}\{(\frac{L}{2})^3-(-\frac{L}{2})^3\}=\frac{M}{3L}(\frac{L^3}{8}+\frac{L^3}{8})
=\frac{M}{3L}.\frac{L^3}{4}
=\frac{ML^2}{12}
আবার,
প্রান্তবিন্দুগামী লম্ব অক্ষের সাপেক্ষে জড়তা ভ্রামক
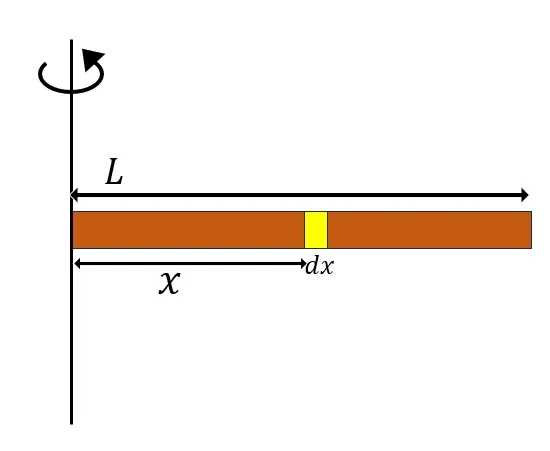
এক্ষেত্রে জড়তা ভ্রামক
I= \int_{0}^{L}{(mdx)x^2}
=\int_{0}^{L}{\frac{M}{L}x^2dx}
=\frac{M}{L}\int_{0}^{L}{x^2dx}
=\frac{M}{L}\left(\frac{x^3}{3}\right)_0^L
=\frac{M}{3L}\left(x^3\right)_0^L
=\frac{M}{3L}(L^3-0^3)
=\frac{M}{3L}L^3
=\frac{ML^2}{3}

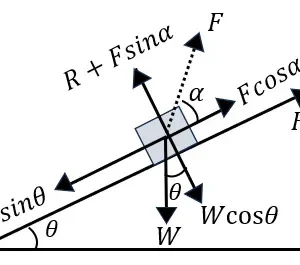









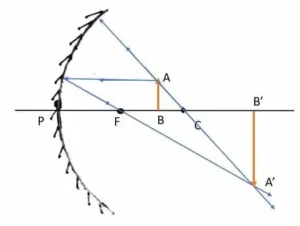

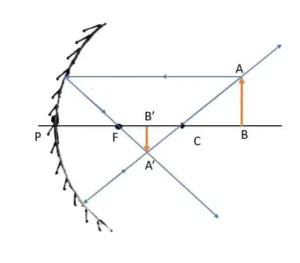



 ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠