Table of Contents
Toggleপরিমাপে বিভিন্ন ধরনের ত্রুটি
শৃঙ্খলাবদ্ধ ত্রুটি (Systematic error), অনিয়মিত ত্রুটি (Random error)।
শৃঙ্খলাবদ্ধ ত্রুটি- পরিমাপ করতে গিয়ে এমন কিছু ঘটে গেল যার জন্য প্রকৃত মান থেকে পৃথক মান পাওয়া গেল তাহলে সেই ধরনের ত্রুটিকে শৃঙ্খলাবদ্ধ ত্রুটি বলে।পরিমাপের সময় ত্রুটিযুক্ত যন্ত্র ব্যবহার করলে, পরিমাপ করার সময় অসচেতনতা কিংবা বাহ্যিক কারণ (তাপমাত্রা, বায়ুপ্রবাহ ইত্যাদি)-এর জন্য শৃঙ্খলা বদ্ধ ত্রুটি তৈরি হয়।
অনিয়মিত ত্রুটি- পরীক্ষার সময় পরীক্ষার শর্তসমূহের তারতম্য এবং পরীক্ষকের ব্যক্তিগত উপলব্ধির তারতম্যের জন্য অনিয়মিত ত্রুটি আসে।
ত্রুটির গণনা
প্রকৃত মান (True Value)- ধরি, কোনো পরীক্ষায় n বার পরিমাপ করে কোনো ভৌত রাশির প্রাপ্ত মানগুলি যথাক্রমে হল x_1, x_2, x_3, …. x_n।
প্রকৃত মান \bar{x}=\frac{x_1+x_2+x_3+\ldots x_n}{n}=\frac{\sum_{i=1}^{n}x_i}{n}
চরম ত্রুটি (Absolute error)- \varepsilon_i=|x_i-\bar{x}|
গড় চরম ত্রুটি বা গড় ত্রুটি (Average error)- \varepsilon=\frac{\sum_{i=1}^{n}\varepsilon_i}{n}
পরীক্ষাধীন রাশির সঠিক মান = \bar{x}\pm\varepsilon
ভগ্নাংশ ত্রুটি বা আপেক্ষিক ত্রুটি বা আনুপাতিক ত্রুটি (Fractional error or Relative error or Proportional error)- \frac{\varepsilon}{\bar{x}}
শতকরা ত্রুটি (Percentage error)- \frac{\varepsilon}{\bar{x}}\times 100
সমক বিচ্যুতি (Standard deviation)- পরিমাপ সংখ্যা (n) খুব বেশি হলে S.D.-এর মান
\sigma=\sqrt{\frac{\sum_{i}\varepsilon_i^2}{n}}
n-এর মান কম হলে \sigma=\sqrt{\frac{\sum_{i}\varepsilon_i^2}{n-1}}
বিভিন্ন ক্ষেত্রে ত্রুটির গণনা
ধরি, A ভৌত রাশিটি x ও y এর ওপর নির্ভরশীল।
যোগ হলে- A=x+y
A নির্ণয়ে সর্বাধিক ত্রুটি \Delta A=\Delta x+\Delta y
বিয়োগ হলে- A=x-y
A নির্ণয়ে সর্বাধিক ত্রুটি \Delta A=\Delta x+\Delta y
গুণ হলে- A=xy
উভয় পাশে ln নিলে হবে, lnA=lnx+lny
অবকল করে পাই- \frac{\Delta A}{A}=\frac{\Delta x}{x}+\frac{\Delta y}{y}
{\frac{\Delta A}{A}|}_{max}=\frac{\Delta x}{x}+\frac{\Delta y}{y}
ভাগ হলে- A=\frac{x}{y}
উভয় পাশে ln নিলে হবে, lnA=lnx-lny
অবকল করে পাই- \frac{\Delta A}{A}=\frac{\Delta x}{x}-\frac{\Delta y}{y}
{\frac{\Delta A}{A}|}_{max}=\frac{\Delta x}{x}+\frac{\Delta y}{y}
বিভিন্ন ঘাতে থাকলে- A=x^ay^b
উভয় পাশে ln নিলে হবে, lnA=alnx+blny
অবকল করে পাই- \frac{\Delta A}{A}=\frac{a\Delta x}{x}+\frac{b\Delta y}{y}
{\frac{\Delta A}{A}|}_{max}=a\frac{\Delta x}{x}+b\frac{\Delta y}{y}











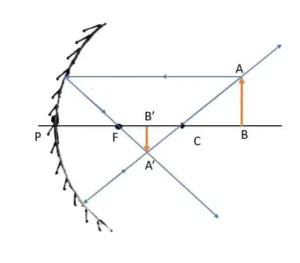



 ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠