1. গোলীয় তলে আলোর প্রতিফলন-অতি সংক্ষিপ্ত প্রশ্নোত্তর
1.1 দুটি সমতল দর্পণ 600 কোণে আনত। সেগুলির মধ্যে আবস্থিত একটি আলোকিত বিন্দু উৎসের প্রতিবিম্বের সংখ্যা-
A) 3 B) 4 C) 5 D) 6
=> সঠিক উত্তর C) 5
ব্যাখ্যা- প্রতিবিম্বের সংখ্যা= \frac{360^0}{\theta^0}-1= \frac{360^0}{60^0}-1=5
1.2 একটি আলোকরশ্মি \frac{1}{2}(\widehat{i} + \sqrt{3}\widehat{j}) অভিমুখে গিয়ে একটি সমতল দর্পণে আপতিত হয়। প্রতিফলনের পর এটি \frac{1}{2}(\widehat{i} - \sqrt{3}\widehat{j}) অভিমুখে যায়। এক্ষেত্রে আপতন কোণ হয়-
A) 300 B) 450 C) 600 D) 750
=> সঠিক উত্তর A) 300 
ব্যাখ্যা- \overrightarrow{u} = \frac{1}{2}(\widehat{i} + \sqrt{3}\widehat{j}) ও \overrightarrow{v} = \frac{1}{2}(\widehat{i} - \sqrt{3}\widehat{j}); এদের মধ্যবর্তী কোণ θ হলে,
\overrightarrow{u}.\overrightarrow{v}=uvcos\theta
or, \frac{1}{2}(\widehat{i} + \sqrt{3}\widehat{j}).\frac{1}{2}(\widehat{i} - \sqrt{3}\widehat{j})=\sqrt{(\frac{1}{2})^2 + (\frac{\sqrt{3}}{2})^2}\ldotp \sqrt{(\frac{1}{2})^2 + (\frac{-\sqrt{3}}{2})^2}\mathrm{\cos}\theta
or, \frac{1}{4}(1-3)=\sqrt{(\frac{1}{4}+\frac{3}{4})}.\sqrt{(\frac{1}{4}+\frac{3}{4})}cos\theta
or, \frac{-2}{4}=1.1cos\theta
or, cos\theta=\frac{-1}{2}
or, cos\theta=cos120^0
or, θ=1200
∴ আপতন কোণ, i=\frac{180^0 -\theta}{2}=\frac{180^0 -120^0}{2}= 300
3. গোলীয় তলে আলোর প্রতিফলন-সংক্ষিপ্ত প্রশ্নোত্তর
3.1 একটি গোলীয় দর্পণের সম্মুখে u দূরত্বে b দৈর্ঘ্যের একটি ক্ষুদ্র বস্তুকে প্রধান অক্ষের সঙ্গে সমান্তরালে রাখা হল। প্রমাণ কর, প্রতিবিম্বের দৈর্ঘ্য = b{(\frac{f}{u-f})}^2, যেখানে f= দর্পণের ফোকাস দৈর্ঘ্য।
=> u = বস্তুর অগ্রভাগের দূরত্ব 
, v= প্রতিবিম্বের অগ্রভাগের দূরত্ব
∴ \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or, \frac{1}{v}=\frac{1}{f}-\frac{1}{u}
or, v=\frac{uf}{u-f}
এখন, বস্তুর পশ্চাদভাগের দূরত্ব = u_1 =u+b, প্রতিবিম্বের পশ্চাদভাগের =v_1 হলে,
\frac{1}{v_1}+\frac{1}{u_1}=\frac{1}{f}
or, \frac{1}{v_1}=\frac{1}{f}-\frac{1}{u_1}
or, \frac{1}{v_1}=\frac{1}{f}-\frac{1}{u+b} = \frac{u+b-f}{(u+b)f}
or, v_1= \frac{(u+b)f}{u+b-f}
প্রতিবিম্বের দৈর্ঘ্য= v_1-v = \frac{u+b-f}{(u+b)f}-\frac{(u+b)f}{u+b-f}
= \frac{(u + b)(u - f) - u(u + b - f)}{(u - f)(u + b - f)}\ldotp f
= \frac{\cancel{u^2} - \cancel{uf} + \cancel{ub} - bf - \cancel{u^2} - \cancel{ub} + \cancel{bf}}{{(u - f)(u + b - f)}}\ldotp f
= - \frac{bf}{(u - f)^2} [\because b ক্ষুদ্র]
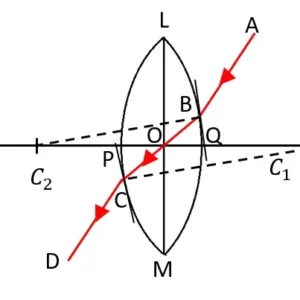
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠
