এই পেজ বা পোস্টটির কোনো অস্তিত্ব নেই।
হোমে যাওয়ার জন্য এখানে ক্লিক করুন।
ফেসবুকে সঙ্গে থাকার জন্য এখানে ক্লিক করুন।
এই পেজ বা পোস্টটির কোনো অস্তিত্ব নেই।
হোমে যাওয়ার জন্য এখানে ক্লিক করুন।
ফেসবুকে সঙ্গে থাকার জন্য এখানে ক্লিক করুন।
\frac{1}{v}+\frac{1}{u}= \frac{1}{f}
or, \frac{u}{v}+1= \frac{u}{f}
or, \frac{1}{n}+1=\frac{u}{f} [\frac{v}{u}=n]
or, u=\frac{(n+1)f}{n}
u=\frac{f}{2} হলে \frac{1}{v}+\frac{1}{u}= \frac{1}{f} সূত্রে মান বসিয়ে পাই
or, \frac{1}{v}-\frac{2}{f}= -\frac{1}{f} [চিহ্নের নিয়ম ব্যবহার করে]
or, \frac{1}{v}=\frac{1}{f} ∴ v=f
∴m=\frac{v}{u}=\frac{f}{-f/2}=-2
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}
or,\frac{1}{v}=-\frac{1}{u}+\frac{1}{f}
\frac{1}{v}– কে y, \frac{1}{u}– কে x ধরলে সমীকরণটি হবে-
y=mx+c যেখানে m=-1 ও \frac{1}{f}=c
সদ্ বস্তু ও তার সদ্ প্রতিবিম্ব প্রতিবিম্বের জন্য v>0 , u>0
m=-1 হলে tanθ=-1 or, θ=1350
ধরি, দুটি উষ্ণতার সেলসিয়াস স্কেলে মান xoC ও y0C।
তাহলে সেলসিয়াস স্কেলে উষ্ণতার পার্থক্য (x-y)oC।
আবার, kelvin স্কেলে xoC= (x+273)K, y0C=(y+273)K
∴ (x-y)oC= {(x+273)-(y+273)}K ={x+273-y-273}K =(x-y)K
অর্থাৎ, সেলসিয়াস স্কেল ও কেল্ভিন স্কেলে উষ্ণতার পার্থক্য সমান হয়।
ধরি, একটি ঘনকের প্রাথমিক দৈর্ঘ্য l_0 । \theta পরিমাণ উষ্ণতা বৃদ্ধিতে দৈর্ঘ্য হয় l_1
দৈর্ঘ্য প্রসারণ গুণাঙ্ক \alpha হলে , l_1=l_0\ (1+\alpha\theta)
or, (l_1)^2=(l_0)^2\ (1+\alpha\theta)^2 [উভয় পাশে বর্গ করে পাই]
or, S_1=S_0(1+2\alpha\theta+\alpha^2\ \theta^2) [ S_0=(l_0)^2 = প্রতি তলের প্রাথমিক ক্ষেত্রফল, S_1=(l_1)^2 = প্রতি তলের অন্তিম ক্ষেত্রফল]
or, S_1\approx(1+2\alpha\theta) [ \alpha <1 হওয়ায় এর উচ্চঘাত উপেক্ষিত]
কিন্তু, S_1=S_0(1+\beta\theta) [ \beta = ক্ষেত্রফল প্রসারণ গুণাঙ্ক]
সুতরাং \beta=2\alpha
আবার, l_1=l_0\ (1+\alpha\theta)
or, (l_1)^3=(l_0)^3\ (1+\alpha\theta)^3 [উভয় পাশে ঘন করে পাই]
or, V_1=V_0(1+3\alpha\theta+3\alpha^2\ \theta^2+\alpha^3\ \theta^3) [ V_0=(l_0)^3 = প্রাথমিক আয়তন, V_1=(l_1)^3 = অন্তিম আয়তন]
or, V_1\approx V_0(1+3\alpha\theta) [ \alpha <1 হওয়ায় এর উচ্চঘাত উপেক্ষিত]
কিন্তু, V_1=V_0(1+\gamma\theta)
সুতরাং, \gamma=3\alpha
\therefore\alpha=\beta/2=\gamma/3
সরল ক্যামেরার গঠন


(i)ক্যামেরার সকল যন্ত্রকে একটি আলোক নিরুদ্ধ বাক্সে রাখা হয়।
(ii)ক্যামেরার এক দিকে একটি উত্তল লেন্স থাকে। তবে ভালো ও উন্নত মানের ক্যামেরায় একাধিক লেন্স বর্তমান। বস্তু থেকে আলোকরশ্মি লেন্স দ্বারা প্রতিসৃত হয়ে ক্যামেরা ভেতরে সদ্, অবশীর্ষ প্রতিবিম্ব তৈরি করে।
(iii) এটি মূলত কয়েকটি ধাতব পাত দ্বারা তোরি গোলাকার ছিদ্র। ডায়াফার্ম দ্বারা আলোর তীব্রতা নিয়ন্ত্রণ করা হয়।
(iv)শাটার দ্বারা আলোক সম্পাতকাল নিয়ন্ত্রণ করা হয়।
(v)প্রতিবিম্বটি যে ফিল্মে পরে সেটি আলোক সংবেদী হয়।
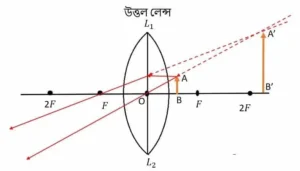
বস্তু- AB
প্রতিবিম্ব- A’B’
বস্তুর অবস্থান- ফোকাস ও আলোককেন্দ্রের মাঝামঝি
প্রতিবিম্বটি- অসদ্ , সমশীর্ষ, বস্তুর তুলনায় বড়

বস্তু- AF
বস্তুর অবস্থান- ফোকাসে
প্রতিবিম্বের অবস্থান- অসীমে
প্রতিবিম্বটি- সদ্ , অবশীর্ষ

বস্তু- AB
প্রতিবিম্ব- A’B’
বস্তুর আবস্থান- f ও 2f এর মাঝামাঝি
প্রতিবিম্বের অবস্থান- 2f এর বেশি দূরত্ব
প্রতিবিম্বটি- সদ্ , অবশীর্ষ, বস্তুর তুলনায় বড়

বস্তু- AB
প্রতিবিম্ব- A’B’
বস্তুর অবস্থান- 2f-এ
প্রতিবিম্বের অবস্থান- 2f-এ
প্রতিবিম্বটি- সদ্ , অবশীর্ষ, বস্তুর সমান
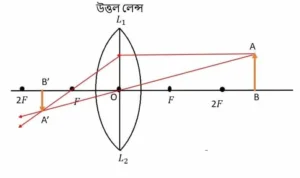
বস্তু- AB
প্রতিবিম্ব- A’B’
বস্তুর অবস্থান- 2f-এর বেশি
প্রতিবিম্বের অবস্থান- f ও 2f এর মাঝামাঝি
প্রতিবিম্বটি- সদ্ , আবশীর্ষ, বস্তুর তুলনায় ছোটো

বস্তু- AB
প্রতিবিম্ব- A’B’
প্রতিবিম্বের অবস্থান- ফোকাস ও মেরুর মাঝামাঝি
প্রতিবিম্বটি অসদ্ ,সমশীর্ষ, বস্তুর তুলনায় ছোটো

বস্তু- AB
প্রতিবিম্ব- A’B’
প্রতিবিম্বের অবস্থান- দর্পণের অভ্যন্তরে
প্রতিবিম্বটি অসদ্ ,সমশীর্ষ, বস্তুর তুলনায় বড়

বস্তু- AF
প্রতিবিম্বের অবস্থান- আসীমে
প্রতিবিম্বটি- সদ্
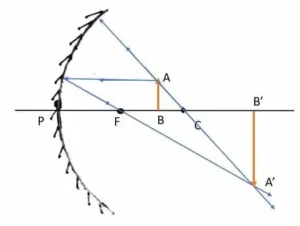
বস্তু- AB
প্রতিবিম্ব- A’B’
প্রতিবিম্বের অবস্থান-বক্রতা কেন্দ্র থেকে দূরে
প্রতিবিম্বটি- সদ্ , আবশীর্ষ, বস্তুর তুলনায় বড়

বস্তু- CA
প্রতিবিম্ব- CA’
প্রতিবিম্বের অবস্থান- বক্রতাকেন্দ্রে
প্রতিবিম্বটি- সদ্, আবশীর্ষ, বস্তুর আকারের সমান
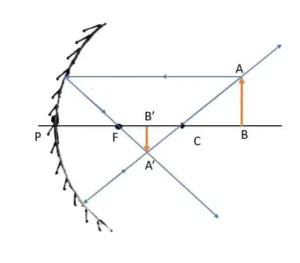
বস্তু- AB
প্রতিবিম্ব- A’B’
প্রতিবিম্বের অবস্থান- ফোকাস ও বক্রতা কেন্দ্রের মাঝামাঝি
প্রতিবিম্বটি সদ্ ,অবশীর্ষ, বস্তুর তুলনায় ছোটো

ABCD একটি আয়তকার কাঁচ ফলক যা বায়ু মাধ্যমে অবস্থিত। PQ রশ্মি BC তলে ∠i_1 কোণে আপতিত হয় এবং ∠r_1 কোণে প্রতিসৃত হয়ে DC তলের R বিন্দুতে পৌছায়। এই তলে আপতন ও প্রতিসরণ কোণ যথাক্রমে ∠r_2 ও ∠i_2। অবশেষে রশ্মিটি প্রতিসৃত হয়ে RS পথে ফলক থেকে নির্গত হয়। Q ও R বিন্দুতে অভিলম্ব যথাক্রমে M_1N_1 ও M_2N_2
∵AB||DC এবং M_1N_1⊥ AB ও M_2N_2⊥ DC
∴M_1N_1||M_2N_2
আবার QR ছেদক।
∴\angle r_1= একান্তর \angle r_2
এখন বায়ু মাধ্যমের সাপেক্ষে কাঁচের প্রতিসরাঙ্ক μ হলে,
μ= \frac{\sin(\angle i_1)}{\sin(\angle r_1)}= \frac{\sin(\angle i_2)}{\sin(\angle r_2)}
or, \sin(\angle i_1)= \sin(\angle i_2)= [∵ \angle r_1= \angle r_2]
∴ i_1=i_2
অর্থাৎ আয়তকার কাঁচ ফলকে আপতন ও প্রতিসরণ কোণ সমাণ। সেজন্য কৌণিক চ্যুতি শূন্য। তবে কিছুটা পার্শ্বীয় সরণ ঘটে।

XY একটি উপাক্ষীয় রশ্মি যা প্রধান অক্ষের সমান্তরাল; MPN অবতল দর্পণ দ্বারা প্রতিফলিত হয়ে রশ্মিটি YZ পথে যায় এবং প্রধান অক্ষের F বিন্দু থেকে আসছে বলে মনে হয়। F হল দর্পণের ফোকাস বিন্দু।
দর্পণটির বক্রতাকেন্দ্র C। বক্রতা ব্যাসার্ধ (PC)=r, ফোকাস দৈর্ঘ্য(PF)=f
আপতন কোণ=∠ i=∠XYB, প্রতিফলন কোণ= ∠r=∠BYZ
∵XY ∥ PC এবং BC ছেদক ∴ ∠XYB = অনুরূপ ∠YCF =∠ i আবার, ∠XYB=বিপ্রতীপ ∠FYC= ∠r
প্রতিফলনের নিয়ম অনুযায়ী, ∠ i = ∠ r
তাহলে ΔCYF এর ∠CYF= ∠YCF
∴ FY=FC …….(1)
আবার XY রশ্মিটি উপাক্ষীয় হওয়ায় P ও Y বিন্দুটি খুব কাছাকাছি অবস্থিত। ∴FY≈ PF ……… (2)
(1)ও (2) নং সমীকরণ তুলনা করে পাই,
PF=FC or, PF=\frac{PC}{2} or, f=\frac{r}{2}
 XY একটি উপাক্ষীয় রশ্মি যা প্রধান অক্ষের সমান্তরাল; MPN অবতল দর্পণ দ্বারা প্রতিফলিত হয়ে রশ্মিটি YZ পথে যায় এবং প্রধান অক্ষের F বিন্দুতে ছেদ করে। F হল দর্পণের ফোকাস বিন্দু।
XY একটি উপাক্ষীয় রশ্মি যা প্রধান অক্ষের সমান্তরাল; MPN অবতল দর্পণ দ্বারা প্রতিফলিত হয়ে রশ্মিটি YZ পথে যায় এবং প্রধান অক্ষের F বিন্দুতে ছেদ করে। F হল দর্পণের ফোকাস বিন্দু।
দর্পণটির বক্রতাকেন্দ্র C। বক্রতা ব্যাসার্ধ (PC)=r, ফোকাস দৈর্ঘ্য(PF)=f
আপতন কোণ= ∠ i= ∠ XYC, প্রতিফলন কোণ= ∠ r= ∠CYZ
∵XY ∥ CP এবং YC ছেদক ∴ ∠XYC = একান্তর ∠YCF = ∠ i
প্রতিফলনের নিয়ম অনুযায়ী, ∠i = ∠r
তাহলে, ΔCYF এর ∠CYF= ∠YCF
∴ FY=FC …….(1)
আবার, XY রশ্মিটি উপাক্ষীয় হওয়ায় P ও Y বিন্দুটি খুব কাছাকাছি অবস্থিত। ∴FY≈ PF ……… (2)
(1)ও (2) নং সমীকরণ তুলনা করে পাই,
PF=FC or, PF=\frac{PC}{2} or, f=\frac{r}{2}
 ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠i_1 আপতিত হয় এবং ∠r_1 প্রতিসৃত হয়ে AC তলের R বিন্দুতে পৌছায়। এখন আপতন ও প্রতিসরণ কোণ যথাক্রমে ∠r_2 ও ∠i_2। এই তলে প্রতিসৃত হয়ে অবশেষে RS পথে প্রিজম থেকে নির্গত হয়।
ABC প্রিজমের প্রতিসারক কোণ ∠A। PQ রশ্মি AC তলে ∠i_1 আপতিত হয় এবং ∠r_1 প্রতিসৃত হয়ে AC তলের R বিন্দুতে পৌছায়। এখন আপতন ও প্রতিসরণ কোণ যথাক্রমে ∠r_2 ও ∠i_2। এই তলে প্রতিসৃত হয়ে অবশেষে RS পথে প্রিজম থেকে নির্গত হয়।
চ্যুতিকোণ δ= ∠UTR
= ∠TQR+ ∠TRQ [∵বহিঃস্থ কোণ = বিপরীত অন্তঃস্থ কোণের সমষ্টি]
= (∠TQV- ∠RQV)+(∠TRV- ∠QRV)
=(∠ i_1 – ∠r_1 )+(∠ i_2 – ∠r_2 )
= (∠ i_1+ ∠ i_2)-(∠r_1 + ∠r_2 ) ……..(1)
এখন, ΔQRV এর ∠RQV+ ∠QVR+ ∠VRQ=180^0
or, ∠r_1+ ∠QVR + ∠r_2 = 180^0 ……….(2)
চতুর্ভূজ AQVR এর ∠RAQ+ ∠AQR+ ∠QVR+ ∠VRA=360^0
or, ∠A+90^0+ ∠QVR+ 90^0= 360^0 [∵ QV⊥ AB ও VR⊥AC]
or, ∠A+ ∠QVR= 180^0 ……… (3)
(2) ও (3) নং সমীকরণ তুলনা করে পাই
∠r_1+ ∠QVR + ∠r_2= ∠A+ ∠QVR
∴ ∠r_1 + ∠r_2= ∠A
(1)নং সমীকরণে ∠r_1 + ∠r_2 এর মান বসিয়ে পাই
\mathbf{δ=∠i_1 +∠ i_2-∠A}
